СТАБИЛЬНОЕ НАСЕЛЕНИЕ (от лат. stabilis - постоянный, неизменный, устойчивый), теоретич. модель нас. с неизменными во времени возрастными интенсивностями рождаемости, смертности и возрастной структурой населения. С. н. предполагается закрытым, т. е. не подверженным миграц. процессам. Применение модели С. н. в демографич. анализе основано на трёх свойствах: 1) С. н. обладает неизменным во времени коэффициентом естественного прироста населения; следовательно, изменение его числ. описывается экспоненциальной функцией времени, а С. н. - частный случай экспоненциального населения. 2) Каждому сочетанию режима рождаемости и порядка вымирания соответствует единственное С. н., с одному ему присущими характеристиками режима воспроизводства населения. 3) У нас., в к-ром с нек-рого момента времени остаются неизменными режим рождаемости и порядок вымирания, постепенно стабилизируется и возрастная структура.
Это свойство наз. сильной эргодичности свойством, а нас. - асимптотически С. н.
С. н. является упрощённым изображением реальных взаимосвязей демографич. процессов и возрастной структуры нас. Теория С. н. позволяет анализировать закономерности воспроиз-ва нас. при разл. гипотезах естеств. прироста населения.
Никакое реальное нас. не является в точном смысле С. н., однако для любого нас. известны длит. временные интервалы, в течение к-рых режим рождаемости и порядок вымирания, подвергаясь тем или иным периодич. или случайным колебаниям, в среднем оставались практически неизменными. Воспроиз-во нас. в этом случае может быть с достаточной точностью описано с помощью модели С. н.
Модель С. н. применяется, во-первых, как основа для расчёта интегральных характеристик режима воспроиз-ва нас., таких, как истинный коэффициент естеств. прироста, истинные коэфф. рождаемости и смертности. Во-вторых, она используется для анализа взаимного влияния режима рождаемости и порядка вымирания, с одной стороны, и возрастной структуры нас.- с другой. В-греть-их, применяется в демографич. расчётах и прогнозах при отсутствии достоверных статистич. данных о нас. (применительно к нас. с относительно неизменным режимом воспроиз-ва). В-четвёртых, используется как составная часть др. демографич. и экон. моделей.
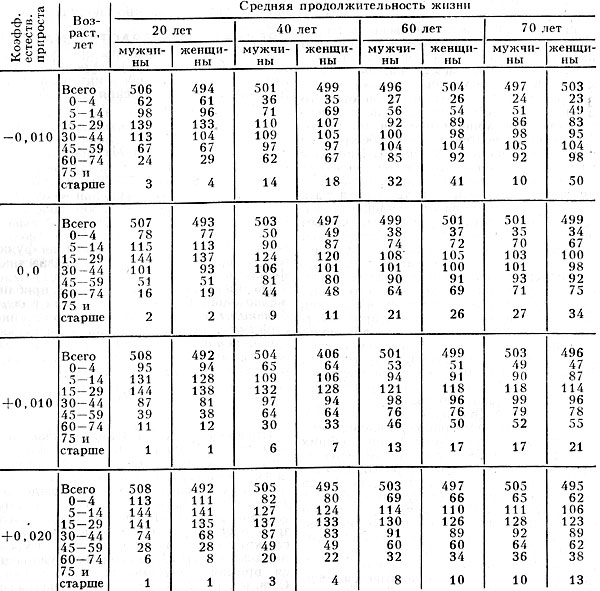
Табл. 1. - Возрастно-половая структура стабильного населения с различными функциями дожития и коэффициентом естественного прироста, o/oo
Существуют непрерывные и дискретные модели С. н. В основе непрерывных лежит интегральное уравнение воспроиз-ва нас., в основе дискретных - матричная модель (см. Модели воспроизводства населения). Модель С. н., как правило, описывает нас. к.-л. одного пола, гл. обр. женское.
Между осн. количеств, характеристиками С. н. существует тесная связь. Для определения всех параметров С. н. достаточно задать функцию рождаемости f(x) и функцию дожития l(х). Коэфф. естеств. прироста С. н. представляет собой единственный действит. корень уравнения 
где lF(x) - функция дожития для жен. нас., fF(x) - функция жен. рождаемости, т. е. вероятность рождения девочки у женщины в интервале возрастов x, x+Δx равна fF(x) Δx.
Числ. С. н. в момент t равна:
P(t) = P(0)ert.
Возрастная структура С. н. описывается функцией с(х):
так что доля лиц в интервале возрастов x1x2 равна 
При одной и той же функции дожития l(х) положит. значениям r соответствует более молодая возрастная структура С. н. и с ростом r состав нас. омолаживается (см. рис. 1). В табл. 1 приведены основные характеристики структуры С. н. при разл. коэфф. естеств. прироста r и функциях дожития, соответствующих типовым таблицам смертности ООН со значением ср. продолжительности жизни при рождении для обоих полов вместе e0 = 20, 40, 60, 70 лет.
Рис. 1. Возрастные пирамиды женских стабильных населений при различных коэффициентах естественного прироста r (o/oo) и одной и той же функции дожития.
Общий коэфф. рождаемости (в) С. н. равен:
Общий коэфф. смертности (m) С. н. равен:
С увеличением коэфф. естеств. прироста r коэфф. рождаемости увеличивается, коэфф. смертности уменьшается (см. рис. 2). Указанные величины равны при r = 0: такое С. н. наз. стационарным населением. Причем в=m=1/e0, где 
- ср. продолжительность жизни при рождении, соответствующая функции дожития l(х).
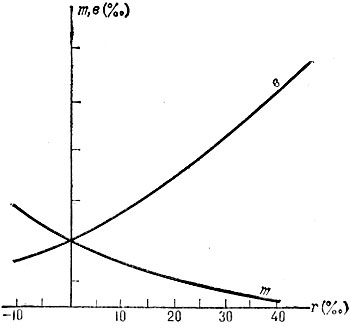
Рис. 2. Зависимость общих коэффициентов рождаемости (в) и смертности (m) от коэффициента естественного прироста в стабильном населении с данной функцией дожития l(x).
Возрастная структура умерших в С. н. описывается функцией d(x): доля умерших в возрастах x1x2 в общем числе умерших равна 
причём
где l'x(x) - производная функции дожития l(х). Число родившихся и число умерших в С. н. меняется в геометрич. прогрессии. Причём число родившихся N(t) = в *P(0)*ert, число умерших M(t) = m*P(0)*ert.
Исходя из связи между количеств. характеристиками С. н., одни из них могут быть восстановлены на основе других (за исключением функции рождаемости, т. к. одно и то же С. н. может возникнуть при разных возрастных интенсивностях рождаемости). Так, для определения коэфф. естеств. прироста r достаточно знать функцию дожития l(х) и возрастную структуру нас. с(х); функцию дожития l(х) и общий коэфф. рождаемости в; функцию дожития l(х) и общий коэфф. смертности m; возрастную структуру с(х) и общий коэфф. смертности m; возрастные структуры нас. и умерших - с(х) и d(x); возрастную структуру умерших d(x) и функцию дожития l(х). Если известны коэфф. естеств. прироста r и одна из трёх функций l(х), с(х), d(x), то этого достаточно для определения двух других из перечисленных функций, общих коэфф. рождаемости и смертности. Эти зависимости справедливы и для экспоненциального нас.
Связь осн. характеристик С. н. с брутто~коэффициентом воспроизводства населения 
и ср. продолжительностью предстоящей жизни при рождении (e0) учитывает фактич. сведения об особенностях кривых рождаемости и дожития со значениями R и e0 в разл. населениях. Проведённый в 60-х гг. экспертами ООН анализ обширных статистич. данных позволил оценить вариацию истинного коэфф. естеств. прироста при фиксированных функциях дожития с различным ео и данном брутто-коэфф. воспроиз-ва R (см. рис. 3) и при фиксированной функции рождаемости f(x) с различными R и данной ср. продолжительностью жизни e0, а также оценить ср. значения r при данных R и e0 (табл. 2).
Рис. 3. Значения коэффициента естественного прироста r, соответствующие различным значениям брутто-коэффициента воспроизводства при неизменных функциях дожития l(x) со средней продолжительностью жизни e0 = 30,4; 51,3; 71,8 лет.
Модель асимптотически С. н. описывает воспроиз-во нас. на этапе, следующем за демографич. революцией, либо после к.-л. катаклизмов, нарушивших его возрастную структуру (войны, эпидемии и т. д.). Для сравнения возрастной структуры реального нас. с возрастной структурой С. н. используются разл. показатели инстабильности. Особенность динамики численности асимптотически С. н. в сравнении со С. н. зависит лишь от начальной возрастной структуры и измеряется потенциалом прироста нас.
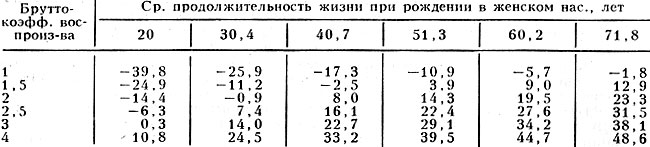
Табл. 2. - Среднее значение истинного коэффициента естественного прироста, o/oo
Обобщения теории С. н. С. н. - центр. элемент системы теоретич. населений, каждое из к-рых характеризуется неизменностью во времени к.-л. характеристик режима воспроиз-ва. Нас., в к-ром неизменны с(х) и l(х), обладает также неизменным коэфф. прироста r и наз. экспоненциальным нас. Ему cooтветствуют все осн. формулы теории С. н., в к-рые не входит функция рождаемости f(x). Экспоненциальное нас. с неизменной функцией рождаемости есть С. н. Нас., в к-ром неизменна только возрастная структура, наз. частично стабильным населением. С. н., у к-рого с определ. момента времени медленно снижаются возрастные показатели смертности, переходит в квазистабильное население.
В табл. 3 приводятся осн. варианты гипотез, определяющих тот или иной тип теоретич. населений. Допуская, что нек-рое реальное нас. достаточно точно соответствует определ. типу теоретич. нас., можно применить систему соотношений количеств. характеристик соответств. модели для практич. расчётов применительно к данному нас. Возможности подобных расчётов существенно увеличиваются с привлечением типовых таблиц смертности и рассчитанных на их основе семейств типовых стабильных (экспоненциальных) населений и типовых квазистабильных нас. Модели С. н. и экспоненциального нас. различаются чисто теоретически. Области их практич. применения совпадают. Соответствующая каждой из таблиц смертности функция дожития l(х) порождает серию типовых стабильных нас. с одинаковой функцией дожития и продолжительностью предстоящей жизни при рождении, но разл. функциями рождаемости и коэфф. естеств. прироста. Серия, как правило, упорядочивается либо значениями истинного коэфф. естеств. прироста, либо брутто-коэфф. воспроиз-ва.
Табл. 3. - Классификация теоретических населений в зависимости от изменения во времени основных характеристик режима воспроизводства
При расчёте характеристик режима воспроиз-ва, числ. и состава нас. стран с неполной или недостоверной демографич. статистикой, относительно к-рого сделано предположение, что оно мало отличается от С. н. (квазистабильного нас.), отбираются известные и оценённые как достоверные показатели состава и воспроиз-ва нас. Они сравниваются с соответств. характеристиками типовых С. н., в результате выбирается наиболее близкое к данному, в смысле тех или иных критериев, типовое С. н.
Рис. 4. Значения коэффициента естественного прироста r, соответствующие различным значениям средней продолжительности жизни при рождении e0 при фиксированных функциях рождаемости с брутто-коэффициентом воспроизводства R=2; 3; 4.
В основе анализа демографич. ситуации с помощью модели С. н. лежит проекция на будущее особенностей воспроиз-ва нас. в нек-рый период времени на основе условного допущения, что возрастные интенсивности рождаемости и смертности в нас. останутся неизменными и спустя нек-рый период нас. превратится в С. н. Характеристики С. н. значительно сильнее, чем параметры реального нас., реагируют на всякое изменение ревариацию общего коэфф. естеств. прироста нас. (см. рис. 5).
Рис. 5. Общий (сплошная линия) и истинный (пунктир) коэффициент естественного прироста населения США.
В С. н. интенсивности рождаемости и смертности для реального и гипотетич. поколений совпадают (см. Продольный анализ, Поперечный анализ). В практике демографич. расчётов преобладают данные для гипогетич. поколения, характеризующие возрастные интенсивности рождаемости и смертности в нас. в нек-рый период времени. На основе этих данных строится модель С. н., к-рая используется в оценке демографич. ситуации. Результаты расчёта для гипотетич. поколения могут в известной мере искажать реальную картину. На рис. 6 изображена динамика нетто-коэфф. воспроиз-ва женского нас. Швеции в 19 в. и в 1-й пол. 20 в. Представленные данные характеризуют нетто-коэфф., рассчитанный для соответств. периодов методом гипотетич. поколения, и нетто-коэфф. реального поколения (когорты) женщин, родившихся за 30 лет до рассматриваемого момента. Обе линии в общих чертах повторяют друг друга. Но результаты когортного расчёта, как правило, ниже, чем данные для гипотетич. поколения, как для отд. лет, так и в среднем за весь период.
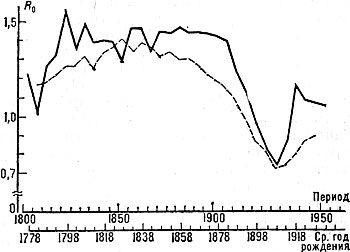
Рис. 6. Нетто-коэффициент воспроизводства женского населения Швеции. Расчёт для гипотетических поколений (сплошная линия) и реальных поколений (пунктир).
С. н. с учётом брачности. Истинный коэфф. естеств. прироста может быть совершенно одинаково рассчитан как для женского, так и для муж. нас. В стабильной ситуации результаты расчётов полностью совпадают, в реальных нас. эти два показателя могут существенно различаться (табл. 4). Так, если допустим, что муж. нас. США росло в соответствии со своим, а женское - со своим коэфф. естеств. прироста, рассчитанным за 1964, то уже через 100 лет мужчин было бы на 19%, а через 200 - на 43% больше, чем женщин. Делаются попытки модифицировать модель С. н. для разрешения этого противоречия.
Табл. 4. - Истинный коэффициент естественного прироста для гипотетического поколения в некоторых странах, o/oo
При расчёте для реального поколения безразлично, учитывается или не учитывается брачность или порядок рождений, эти факторы не влияют на итоговые показатели и на параметры модели С. н. При расчёте для гипотетич. поколения конечный результат существенно зависит от того, принимаются ли неизменными сами возрастные интенсивности рождаемости или же интенсивности брачности, брачной и внебрачной рождаемости, рождаемости по очерёдности рождений и т. д.
Известны попытки построить С. н. с учётом семейной структуры, включить в модель социально-демографич. характеристики (образовательные, профессиональные и т. д.). Для этого необходимо определить возрастные интенсивности перехода из одной социально-демографич. группы в другую, приняв их неизменными в будущем. Если стабильность интенсивностей демографич. процессов достаточно правдоподобна, то стабильность интенсивностей социальных перемещений проблематична. Отсюда вытекает т. н. обратная задача теории С. н., в к-рой исходя из представляющейся оптимальной социально-демографич. структуры пытаются найти возрастные интенсивности переходов, обеспечивающие формирование данной структуры.
Другим обобщением модели С. н. являются С. н. с учётом миграции. В основе лежит не отказ от исходной концепции закрытого нас., а рассмотрение отд. его частей - субнаселений, связанных миграц. потоками с неизменными возрастными интенсивностями выезда. Эти модели позволяют, хотя и приближённо, измерить роль каждого из трёх процессов: рождаемости, смертности, миграции в формировании числ. и состава нас.
Идея экспоненциального роста населений как основы С. н. впервые высказана англ. актуарием М. Хейлом (1677). В 1693 Э. Галлей опубликовал таблицу смертности для нас. г. Бреславль (совр. Вроцлав) за 1687-91, к-рую можно рассматривать как первую попытку построения теоретич. стационарного нас.
В 1760 Л. Эйлер установил взаимосвязи между численностями возрастных совокупностей живущих и умерших в нас. с неизменным порядком вымирания, в к-ром число родившихся растёт как экспоненциальная функция времени. Эти взаимосвязи легли в основу Эйлера метода построения таблиц смертности. Эйлер - автор концепции закрытого нас. Экспоненциальный рост у Эйлера - логич. следствие разл. гипотез о рождаемости и смертности. Ему принадлежит одна из первых попыток упрощённого, но учитывающего рождаемость описания воспроиз-ва нас. (1741); т. о. модель экспоненциального роста у Эйлера уже в какой-то мере обоснована неизменностью отд. компонентов воспроиз-ва. В 1868 нем. статистик Г. Кнапп завершил разработку теории стационарного нас. как частного случая экспоненциального нас., вне связи с вопросом о рождаемости. Следом за Эйлером включил рождаемость в описание воспроиз-ва нас. В. Лексис, заложивший основу для расчёта показателей воспроиз-ва и гл. обр. нетто-коэфф. воспроиз-ва. Р. Бек исчислил нетто- и брутто-коэфф. воспроизводства населения Берлина (1884) и построил первую таблицу рождаемости.
Завершение разработки теории С. н. относится к 1-й трети 20 в. В работах А. Дж. Лотки (1907) и В. Борткевича (1911) в окончат. варианте создана теория экспоненциальных нас., т. е. задача, к-рую Кнапп решил в случае неизменной числ. нас., решена для нас., растущего в геометрич. прогрессии. Р. Кучипский в работах 1907-35 широко ввёл в науч. обиход нетто- и брутто-коэфф. воспроиз-ва Бека. Создание собственно теории С. н. связано с именем амер. демографа Лотки, к-рым в работах 1907-39 (и позднее - до 1948) изложены все осн. положения теории и свойства С. н.
Лотка разработал теорию С. н. в непрерывной форме, при этом в его доказательстве свойства эргодичности остался ряд нерешенных вопросов. Амер. математик У. Феллер (1941) уточнил условия, при к-рых указанное доказательство справедливо, и предложил дискретный подход к теории С. н. Идя по предложенному Феллером пути, П. Лесли (Австралия, 1946) построил дискретную теорию С. н. средствами матричной алгебры. Этому результату предшествовали попытки опровергнуть свойство эргодичности на дискретном уровне Бернардалли, в основе к-рых лежали весьма условные гипотезы о форме кривой рождаемости f(x), в частности полагалось, что все рождения концентрируются в одном возрастном интервале.
Лотка построил С. н. для одного пола. П. Венсан (Франция, 1946), Дж. Хаджнал (1947) и П. Кармел (1948; оба - Великобритания) в своих работах указали на возможные противоречия между муж. и жен. мерами воспроиз-ва и попытались построить модель С. н. для обоих полов. Обобщение теории С. н. путём включения кроме возраста и др. характеристик связано с работами К. Джини, Кармела, Ж. Буржуа-Пиша и Л. Анри (Франция), Н. Кейфица (США), А. Я. Боярского (СССР). Одним из обобщений теории С. н. явились модели воспроиз-ва с учётом миграции. Швед. демограф X. Хюрениус (1954) наряду с интенсивностью смертности учитывал интенсивность чистой миграции. А. Роджерс (США) и В. Ф. Шукайло (СССР) в 70-х гг. рассмотрели воспроиз-во в системе населений, связанных миграц. потоками.
Большой вклад в разработку методов практич. применения С. н. внесли сов. демографы С. А. Новосельский, В. В. Паевский, Боярский, И. Г. Венецкий и др.
Совр. этап развития теории С. н. связан с обобщением осн. выводов на случай демографич. процессов с переменными интенсивностями. А. Коул (1957) и А. Лопес (1961; оба - США) доказали свойство слабой эргодичности при меняющихся интенсивностях рождаемости и смертности. Динамика числ. нас. в период стабилизации рассмотрена Буржуа-Пиша (см. Потенциал прироста населения). В публикации ООН в 1958 впервые появилось понятие квазистабильного нас., в 1966 - положено начало теории частично С. н., развитого в последующих работах Буржуа-Пиша (1971).
Осн. характеристики типовых С. н., рассчитанных на основе типовых таблиц смертности, даны в серии публикаций ООН 1956-66, 1982.
Венецкий И. Г., Математические методы в демографии, М. 1971; Боярский А. Я., Население и методы его изучения, М. 1975, с. 78-97, 117 - 25; Пирожков С. И, Демографические процессы и возрастная структура населения, М. 1976; Таба Л., Взаимосвязи между возрастной структурой, плодовитостью, cмертностью и миграцией, пер. с англ., в кн : Демографические модели, М. 1977; Буржуа-Пиша Ж., Стабильные, полустабильные населения и потенциал роста, [пер. с англ.], там же; Concept de la population stable, N. Y., [1366]; Methods of estimating basic demographic measures from incomplete data, N. Y., 1967; Keytitz N., Introduction о the mathematics of population, Reading (Mass.) - L., 1968; Соale A, The growth and structure of human populations, Princeton, 1972.
E. М. Андреев.
Демографический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор Д.И. Валентей. 1985.