Akademik

- понятие теории расширений полей. Пусть Кнек-рое расширение поля k. Элементы наз. алгебраически независимыми над k, если для всякого не равного тождественно нулю многочлена 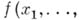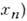с коэффициентами из поля k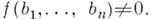. В противном случае элементы наз. алгебраически зависимыми. Бесконечное множество элементов наз. алгебраически независимым, если независимо каждое его конечное подмножество, и зависимым в противном случае. Определение А. н. может быть распространено на случай, когда К- кольцо и k - его подкольцо (см., напр., [1]).

Алгебраическая независимость чисел. Комплексные числа наз. алгебраически независимыми, если они алгебраически независимы над полем алгебраич. чисел, т. е. для любого многочлена 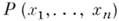с алгебраич. коэффициентами, из к-рых не все равны нулю, имеет место 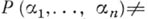ф В противном случае наз. алгебраически зависимыми. Понятие А. н. чисел является обобщением понятия трансцендентности числа (случай n=1). Если несколько чисел алгебраически независимы, то каждое из них трансцендентно. Доказательство А. н. каких-либо чисел сопряжено обычно с большими трудностями. Существующие аналитич. методы в теории трансцендентных чисел позволяют решать эту проблему для значений нек-рых классов аналитич. функций. Так, установлено, что значения показательной функции при алгебраических линейно независимых над полем рациональных чисел значениях аргумента алгебраически независимы. Аналогичный результат получен для функций Бесселя (см. Зигеля метод). Установлен также ряд общих теорем об А. н. значений в алгебраич. точках E-функций, удовлетворяющих линейным дифференциальным уравнениям с коэффициентами из поля рациональных функций [2], [3]. Доказана А. н. чисел 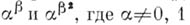- алгебраич. число, а - кубическая иррациональность, и, кроме того, ряд теорем об алгебраич. невыражаемости чисел-понятий, близком к понятию А. н.

Качественному понятию А. н. чисел можно придать количественную характеристику, если рассмотреть алгебраической независимости меру этих чисел. Упомянутые аналитич. методы позволяют получать оценки снизу для меры А. н. нек-рых классов чисел. Установлены общие теоремы об оценке меры А. н. значений Я-функций [3].

Лит.:[1] Лен г С., Алгебра, пер. с англ., М., 1968; [2] Фельдман Н. И., Шидловский А. Б., "Успехи ма-тем. наук", 1967, т. 22, в. 3, с. 3-81; [3] Шидловский А. В., "Труды Матем. ин-та АН СССР", 1973, т. 132, с. 169-202.

А. Б. Шидловский.