Akademik

- 1) Обобщение понятия обычной поверхности трехмерного пространства на случай n-мерного пространства. Размерность Г. на единицу меньше размерности объемлющего пространства.

2) Если - дифференцируемые многообразия, и определено погружение то - Г. в N. Здесь f - дифференцируемое отображение, дифференциал к-рого в любой точке является ннъективным отображением пространства М _х , касательного к Мв точке х, в пространство N_f(x) , касательное к Nв точке 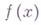. В. Т. Базылев.

3) Г. алгебраическая- подмногообразие алгебраич. многообразия, локально задаваемое одним уравнением. Г. а. в аффинном пространстве над полем kзадается глобально одним уравнением

Г. a. Wв проективном пространстве задается уравнением

где F - однородная форма от переменных. Степень тп этой формы наз. степенью (порядком) гиперповерхности. Замкнутая подсхема Wсхемы Vназ. гиперповерхностью, если соответствующий пучок идеалов является пучком главных идеалов. Для связных неособых алгебраич. многообразий это условие означает, что коразмерность W в V равна единице. Для каждой неособой Г. а. порядка m (обозначаемой часто через ) имеют место следующие факты:

канонич. класс равен - класс гиперплоского сечения W:

группы когомологий 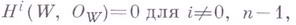а

при фундаментальная группа (алгебраическая или топологическая, если ) ;

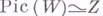при группа Пикара и порождается классом гиперплоского сечения. И. В. Долгачев.

4) Г. аналитическая (Г. а.) - множество Sв комплексном евклидовом пространстве , к-рое в окрестности каждой своей точки задается уравнением где функция непрерывна по параметру и при каждом фиксированном tголоморфна по z в независящей от tокрестности причем для всех .

Другими словами, Г. а. есть множество в , к-рое локально является объединением непрерывного однопара-метрич. семейства комплексноаналитич. поверхностей комплексной коразмерности 1. Напр., если функция f голоморфна в области и grad в D, то множества и т. п. являются Г. а.

Дважды гладкая гиперповерхность в является Г. а. тогда и только тогда, когда ее форма Леви тождественно на Sравна нулю или когда Sлокально псевдовыпукла с обеих сторон. Е. М. Чирка