Akademik

- плоская алгебраич. кривая 3-го порядка, уравнение к-рой в декартовых прямоугольных координатах имеет вид: x³+y³-3axy=0, параметрические уравнения

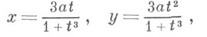
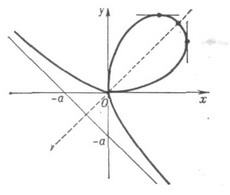
где t- тангенс угла между радиус-вектором кривой и осью Ох. Д. л. симметричен относительно биссектрисы у = х( см. рис.). В точках с координатам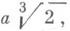и (

) и (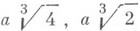) касательные параллельны координатным осям. Начало координат - узловая точка с касательными, по к-рым проходят оси координат. Асимптота: у= -х- а. Площадь между кривой и асимптотой: 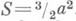. Площадь петли: Д. л. назван по имени Р. Декарта (R. Descartes), впервые его рассмотревшего в 1638.

Лит.:[1] Савелов А. А.. Плоские кривые, М., 1960; [2] Смогоржевский А. С, Столова Е. С, Справочник по теории плоских кривых третьего порядка, М., 1961.

Д. Д. Соколов.