- способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов (и вообще, двух элементов евклидова, кольца )или общей меры двух отрезков. Описан в геометрич. форме в "Началах" Евклида (3 в. до н. э.).
Для случая положительных целых чисел 
этот способ состоит в следующем. Деление с остатком числа ана число b всегда приводит к результату a=nb+b1, где частное п- целое положительное число, а остаток b1 либо 0, либо положительное число, меньшее b, 
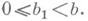Производится последовательное деление:
где все ni - положительные целые числа и 
до тех пор, пока не получится остаток, равный 0. Ряд равенств (*) закончится так:
Последний положительный остаток bk в этом процессе и является наибольшим общим делителем чисел аи b. Е. а. для многочленов или отрезков аналогичны Е. а. для целых чисел. В случае несоизмеримых отрезков применение Е. а. приводит к бесконечному процессу.
БСЭ-3.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.