Akademik

-1) Наименьшее из натуральных чисел:1. При умножении любого числа на 1 получается то же самое число.

2) Элемент емножества Мназ. левой (правой) единицей по отношению к бинарной алгебраической операции *, определенной на множестве М, если для цюбого элемента выполняется равенство

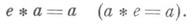
Если существуют хотя бы одна левая Е. и хотя бы одна правая Е., то они совпадают и других Е. нет. Если на множестве Мопределено несколько бинарных операций (напр., сложение и умножение в кольце), то Е. наз. только Е. по отношению к одной из этих операций, обычно по отношению к умножению. Е. по отношению к сложению наз. тогда нулем.

3) Единицей решетки (структуры) наз. ее наибольший элемент, т. е. Е. относительно операции объединения.

4) Единицей, или делителем единицы, области целостности Кназ. всякий ее обратимый элемент, т. е. такой элемент е, для к-рого существует обратный e^-1 и ee^-1=1. Все Е. области целостности образуют группу по умножению. Эта же терминология иногда сохраняется и при переходе к полю частных кольца K (т. е. единицами поля частных наз. Е. самого кольца К). Напр., Е. поля алгебраич. чисел кназ. единицы кольца целых алгебраич. чисел поля k, р -адическими Е. наз. единицы кольца целых р-адических чисел и т. д.

5) Единичный морфизм объекта в категории иногда наз. просто единицей.

О. А. Иванова.