в топологическом пространстве - множество, содержащее все свои предельные точки. Таким образом, все точки дополнения к 3. м.- внутренние, и потому 3. м. можно определить как дополнение к открытому. Понятие 3. м. лежит в основе определения топологич. пространства как непустого множества Xс заданной системой множеств (называемых замкнутыми), удовлетворяющей аксиомам: все Xи пустое множество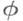 
замкнуты; пересечение любого числа 3. м. замкнуто; объединение конечного числа 3. м. замкнуто.
Лит:[1] Куратовский К., Топология, [пер. с англ.], т. 1, М., 1966.
А. А. Мальцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.