Akademik

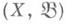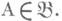- 1) И. м. в измеримом пространстве относительно измеримого преобразования Тэтого пространства - такая мера m на что m(A)=m(T^-1A). для всех Обычно подразумевается, что мера конечная (т. е. или по крайней мере cr-конечная (т. е. Xможно представить в виде счетного объединения 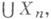где. В наиболее важном случае, когда Т- биекция и отображение T^-1 тоже измеримо (тогда говорят, что Тобратимо, имея в виду обратимость в классе измеримых преобразований), инвариантность меры m эквивалентна тому, что m(A)=m(TA). для всех Наконец, И. м. для семейства (измеримых) преобразований - полугруппы, группы, потока и т. д.- называется мера, инвариантная относительно всех преобразований из этого семейства. Понятие И. м. играет важную роль в теории динамич. систем и эргодич. теории. В последней рассматриваются различные свойства динамич. систем в пространстве с мерой имеющих m. своей И. м. Если динамич. система имеет несколько И. м., напр. m и v, то ее свойства как системы в (X, B, m) (свойства по отношению к И. м. m) могут отличаться от ее же свойств как системы в (свойств по отношению к v). Когда у фиксированной динамич. системы рассматриваются разные И. м., то о свойствах системы относительно И. м. и. часто говорят короче как о свойствах меры и. (напр., "эргодичность m" означает эргодичность данной системы как системы в (X, B,m), т. е. отсутствие инвариантных множеств и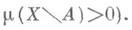

Исторически первые примеры И. м. связаны с дифференциальными свойствами преобразований, образующих потоки нек-рых специальных типов на гладких многообразиях (см. Гамильтонова система, Интегральный инвариант). В терминах (локальных) координат х _г, . . ., х _п эти меры и. представляются в виде dm=rdx₁ ... dx_n, причем имеются явные выражения для плотности r=r(x₁, ..., х _п). В примерах алгебраич. происхождения (групповые сдвиги и т. д.) И. м. часто является мера Хаара или мера, получающаяся из нее с помощью какой-нибудь естественной конструкции.

В топологич. динамике Н. Н. Боголюбовым и Н. М. Крыловым ([1], см. также [2], [3]) доказано существование конечных эргодич. И. м. для непрерывных потоков и каскадов на метрич. компакте X(возможны нек-рые обобщения [4], [5], [6]). Неэргодические конечные И. м. являются, в нек-ром смысле, линейными комбинациями эргодических; носители конечных И. м.. определенным образом связаны с поведением траекторий в X(все эти И. м. сосредоточены на так наз. минимальном центре притяжения [3]). Не приходится рассчитывать на более подробные утверждения о свойствах И. м. в общем случае - они могут быть совсем различными. Так, в одном случае эргодич. И. м. может быть сосредоточена в одной точке, в другом - быть положительной для всех открытых подмножеств Xи обладать свойствами "квазислучайного" характера (перемешивание, положительная энтропия и т. д.), описание и исследование к-рых относится к эргодич. теории (тогда как обращение к последней в предыдущем случае было бы бессодержательным). Поэтому имеется ряд исследований о существовании И. м. с теми или иными интересными свойствами у динамич. систем того или иного специального типа.

Наконец, возможна чисто метрич. постановка вопроса об И. м. Пусть динамич. система имеет квазиинвариантную меру m; существует ли у нее И. м. v, эквивалентная m? (Обсуждение этой постановки вопроса см. в [7]. О другой постановке см. [8]). Ответ в общем случае отрицательный, даже если требовать только s-конечности v, a- Лебега пространство [9]. Известны различные варианты необходимых и достаточных условий существования конечной И. м.; наиболее удачными представляются условия Хаджана

И Какутани [10], [8].

Д. В. Аносов,

2) И. м. в теории вероятностей определяется относительно переходной вероятности. Пусть - измеримое пространство, где Аесть s-алгебра, и Р( х, А), - переходная вероятность (т. е. Р( х, Х), есть вероятностная мера на 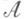при каждом и Р(Х, А)- измерима относительно при каждом . Счетно-аддитивная мера m, на наз. инвариантной относительно Р, если

Если Т- измеримое отображение в себя, то мера m инвариантна относительно Ттогда и только тогда, когда она инвариантна относительно переходной вероятности Р( х, А) = c_T(x)(A), где c _у(A)=1 при и c _у (А) = 0 при