Akademik

решения проблемы собственных значений матрицы - методы нахождения собственных значений и собственных векторов (или корневого базиса) матрицы, минующие предварительное вычисление характеристич. многочлена. Эти методы существенно различаются для задач среднего размера, матрицы к-рых могут быть целиком размещены в оперативной памяти вычислительной машины, и для задач большого порядка, в к-рых хранение информации обычно осуществляется в компактной форме.

Первый И. м. был предложен К. Якоби [1] для вычисления собственных значений и векторов действительных симметричных матриц (см. Вращений метод). Метод переносится на комплексные эрмитовы матрицы, а также на более широкий класс нормальных матриц.

Имеется ряд обобщений метода Якоби для матриц произвольного вида. Типичный алгоритм этого класса состоит из последовательности элементарных шагов, выполняемых по схеме:

При этом роль подобного преобразования с (элементарной) матрицей S_k состоит в уменьшении евклидовой нормы текущей матрицы А _k, т. е. в приближении ее к нек-рой нормальной матрице. В качестве Т _k обычно берется матрица вращений или ее унитарный аналог. Смысл подобного преобразования с этой матрицей, как и в классич. методе Якоби, заключается в аннулировании внедиагонального элемента в нек-рой эрмитовой матрице, связанной с матрицей А _k+1, напр, в матрице С ростом kматрицы А _k сходятся к матрице диагонального или квазидиагонального вида, а накопленное произведение матриц S_k и Т _k дает матрицу, столбцами к-рой являются приближенные собственные векторы либо векторы, образующие базисы инвариантных подпространств матрицы (см. [2], [3]).

продолжение Итерационные методы...

Наряду с вышеописанными методами развиваются алгоритмы другого класса, так. наз. степенные методы. Самым эффективным методом этого направления, наиболее широко применяющимся для решения задач среднего размера, является QR -алгоритм (см. [4], [5]). Итерации QR-алгоритма проводятся по следующей схеме:

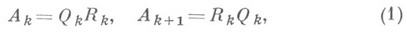
здесь Q_k- ортогональная или унитарная, a R_k- правая треугольная матрица. Для перехода от А _k к A_k+1 сначала находится ортогонально-треугольное разложение матрицы А и, после чего матрицы Q_k и R_k перемножаются в обратном порядке. Если положить R_k=R_k ...R₁, то из (1) следует схема

Таким образом, QR-алгоритм генерирует последовательность матриц А _k, ортогонально подобных исходной' матрице А ₁;при этом трансформирующая матрица 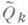является ортогональной компонентой в разложении (2) матрицы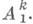

При итерации по схеме (1) матрицы А _k сходятся к правой треугольной или квазитреугольной матрице, причем скорость сходимости поддиагональных элементов к нулю управляется отношениями модулей различных собственных значений и является, вообще говоря, довольно медленной. Для ускорения сходимости QR- алгоритма используются так наз. сдвиги, что приводит к следующему видоизменению схемы (1):

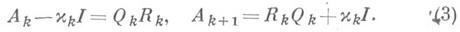
Обычно применение сдвигов (напр., x_k=а _nn^(k) )позволяет, получить быструю сходимость внедиагональных элементов последней строки к нулю (асимптотически квадратичную в общем случае и кубическую для эрмитовых матриц) и соответственно быструю стабилизацию диагонального элемента ( п, п). После того, как значение этого элемента установилось, дальнейшие итерации проводят с главной подматрицей порядка n-1, и т. д. Собственные векторы результирующей треугольной матрицы после умножения на накопленное произведение ортогональных матриц Q_k дают собственные векторы исходной матрицы А ₁.

Итерации по схеме (1) либо (3) применяют к матрице, предварительно приведенной к так наз. форме Хессенберга. Говорят, что матрица Аимеет правую форму Хессенберга, если а _ij=0 при i>j+l. QR-алго ритм обладает свойством сохранять форму Хессенберга исходной матрицы, что намного удешевляет стоимость каждой итерации. Есть и другие важные возможности уменьшения объема вычислений, напр., неявное использование сдвигов, что позволяет находить комплексно сопряженные собственные значения действительных матриц, не прибегая к комплексной арифметике.

В задачах высокого порядка (от нескольких сотен до нескольких тысяч) матрицы обычно бывают разреженными, т. е. имеют относительно небольшое число ненулевых элементов. При этом, как правило, нужно вычислять не все, а лишь несколько собственных значений и соответствующие собственные векторы. В типичном случае требуемые собственные значения - наибольшие или наименьшие по модулю.

Описанные выше методы, основанные на подобных преобразованиях, разрушают разреженность матрицы и потому неприемлемы. Основными для задач высокого порядка являются методы, элементарная операция которых - умножение матрицы на вектор. При их описании в дальнейшем предполагается, что собственные значения заданной матрицы А занумерованы в порядке убывания модулей так, что

Наиболее широкую область применимости имеет степенной метод для вычисления собственного значения l₁ с максимальным модулем. Исходя из начального приближения х ₀ строится последовательность нормированных векторов

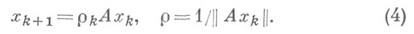
Эта последовательность сходится к собственному вектору, отвечающему l₁, при выполнении следующих условий: 1) все элементарные делители матрицы А, относящиеся к l₁,- линейные; 2) нет других собственных значений с тем же модулем; 3) в разложении исходного вектора х ₀ по корневому базису матрицы Аимеется нетривиальная компонента по собственному подпространству для l₁. Однако сходимость степенного метода, как правило, медленная и определяется отношением величин двух старших по модулю собственных значений.

Если известно приближение 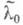к желаемому собственному значению l_i, то быстрая сходимость может быть достигнута посредством метода обратных итераций. Вместо (4) строится последовательность, определяемая соотношениями

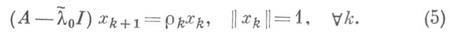
Метод обратных итераций есть по существу степенной метод для матрицы 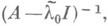имеющей сильно доминирующее собственное значение Реализация формулы (5) требует, однако, решения линейной системы с матрицей 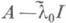и даже при использовании специальных методов для разреженных систем предъявляет повышенные требования к оперативной памяти по сравнению со степенным методом.

Для вычисления группы собственных значений применяются так наз. методы одновременных итераций. Они представляют собой обобщение степенного метода, где вместо итераций одного вектора фактически строятся итерации матрицей Ацелого подпространства. Типичным для этой группы методов является метод Стьюарта [6]. Пусть собственные значения матрицы Аудовлетворяют соотношениям

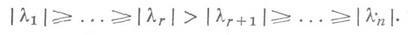
Выбирается начальная п r-матрица Q₀ с ортонормированными столбцами. Исходя из Q₀, строится последовательность матриц Q_k по схеме:

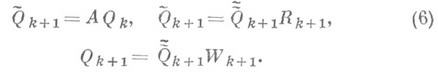
Во второй из этих формул R_k+1 - правая треугольная r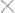r-матрица, а матрица имеет ортонормированные столбцы. Цель этого разложения, к-рое может выполняться не на каждой итерации, состоит в том, чтобы обеспечить линейную независимость столбцов последовательно получаемых матриц Q_k, к-рая в практическом смысле может быть утеряна в результате многократного итерирования матрицей А. Важную роль в ускорении сходимости метода играет третья формула (6). Ортогональная rr- матрица, участвующая в этой формуле, имеет следующий смысл. Если обозначить через В _k+1 rr-матрицу Q^*_kAQ_k, то W_k+1 приводит В _k+1 к форме Шура, т. е. правой треугольной матрице. Матрица W_k+1 может быть построена посредством QR- алгоритма; ее столбцы образуют базис Шура матрицы B_k+1, характеризуемый тем, что при любом к,линейная оболочка первых kвекторов есть инвариантное подпространство матрицы B_k+1. Матрицы Q_k метода Стьюарта сходятся к матрице Q, столбцы к-рой дают базис Шура для инвариантного подпространства матрицы А, отвечающего собственным значениям l₁, ..., l_r. При этом скорость сходимости i-ro столбца определяется отношением |l_r+1|/|l_i|.

В случае действительной симметричной матрицы появляются дополнительные возможности, связанные с трактовкой собственных значений как стационарных точек функционала Рэлея:

Для нахождения крайних точек спектра могут быть применены методы безусловной оптимизации функционала (7). Получающаяся здесь теория параллельна теории итерационных методов для решения положительно определенных линейных систем и приводит к тем же самым алгоритмам: координатной релаксации, последовательной сверхрелаксации, наискорейшего спуска, сопряженных градиентов (см. [7]).

Перечисленные методы находят собственные значения "по одному". Для одновременного вычисления группы собственных значений симметричной матрицы используется метод Ланцоша [8], к-рый предназначался для трехдиагонализации симметричной матрицы порядка п. В основу метода положено следующее наблюдение: если последовательность векторов р ₀, А _р0,..., 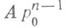линейно независима, то в базисе q₁, q₂,..., q_n, полученном из нее процессом ортонормализации, матрица приводится к трехдиагональной форме Т _п. Векторы q_k строятся по трехчленным рекуррентным формулам

коэффициенты a_k и b_k, k=l, . . ., п, определяют матрицу Т _п. После кшагов процесса ортогонализации известны' векторы q₁,. . ., q_k и главная подматрица Т _k матрицы Т _n. Во многих случаях уже при часть собственных значений матрицы Т _k достаточно точно приближает нек-рые собственные значения Т _п;. соответствующие собственные векторы Т _k могут быть использованы для построения приближений к собственным векторам А. Если же достигнутая точность еще не удовлетворительна, то можно выбрать новое начальное приближение в линейной оболочке векторов q₁, ..., q_k и повторить процесс, проведя шагов, и т. д. В этом и состоит итерационная трактовка метода Ланцоша (см. [9]). Нахождение внутренних точек спектра для разреженных матриц высокого порядка еще не имеет удовлетворительного численного решения.

Лит.:[1] Jасоbi С. G., "J. reine und angew. Math.", 1846, Bd 30, .Mi 1, S. 51-94; [2] Eberlein P., J., "J. Soc. Industr. and Appl. Math.", 1962, v. 101, № 1, p. 74-88; [3] Воеводин В. В., "Вычисл. методы и программирование", 1965, N" 3, с. 89 - 105; [4]КублановскаяВ. Н., "Ж. вычисл. матем. и матем. физ.", 1961, т. 1, !Ns 4,'с. 555-70; [5] Francis J. G. F., "Comput. J.", 1961, v. 4, Mb 3, p. 265-71; 1962. v. 4, № 4, p. 332-45; [6] Stewart G. W., "Numer. Math.", 1976, v. 25, ЛЬ 2, p. 123-36; [7] Ruhe A., Computation of engenvalues and eigenvectors, В., 1977; [8] Lanczos C, "J. Res. Nat. Bur. Standards", 1950, v. 45, Mb 4, p. 255-82; [9] Paige С. С, "J. Inst. Math, and Appl.", 1972, v. 10, p. 373-81.

X. Д. Икрамов.