Akademik

- матрица, образованная из попарных ковариаций нескольких случайных величин; точнее, для k-мерного случайного вектора X=(X₁,. .., X_k )К. м. наз. квадратная матрица

где -вектор средних значений. Компоненты К. м. равны

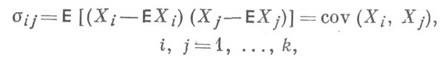
и при i=j совпадают с DX_i (т. е. на главной диагонали К. м. находятся дисперсии величин X,). К. м. представляет собой симметричную неотрицательно определенную матрицу. Если К. м. является положительно определенной, то распределение X- невырожденное распределение, в противном случае - вырожденное. Для случайного вектора XК. м. играет роль дисперсии. Если дисперсии случайных величин X₁. . ., X_k равны 1, то К. м. для вектора Х=( Х ₁,. . ., X _k )совпадает с корреляционной матрицей.

Выборочная К. м. для выборки X⁽¹⁾, ..., Х ^{п), где Х ^(m),m=1,..., n- независимые одинаково распределенные случайные k-мерные векторы, состоит из оценок дисперсий и ковариаций:

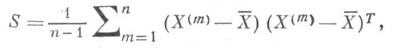
где 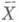- вектор арифметического среднего Х ⁽¹⁾,..., Х ⁽ⁿ⁾. Если случайные векторы Х ⁽¹⁾, ..., Х ⁽ⁿ⁾ имеют нормальное распределение с К. м. 2, то Sявляется оценкой максимального правдоподобия е; в этом случае совместное распределение элементов матрицы (п-1)Sназ. Уишарта распределением, оно является одним Из основных распределений в многомерном статистич. анализе, с помощью к-рого проверяются гипотезы о К. М. е.

А. В. Прохоров.