Akademik

G над R - комплексная группа Ли G _С, содержащая Gв качестве вещественной подгруппы Ли и такая, что алгебра Ли 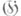группы Gявляется вещественной формой алгебры Ли группы (см. Комплексификация ал гебра Ли). Группа Gпри этом наз. вещественной формой группы Ли G _С. Напр., группа U(п)всех унитарных матриц порядка пявляется вещественной формой группы GL ( п, С) всех невырожденных матриц порядка пс комплексными элементами.

Имеется взаимно однозначное соответствие между комплексно аналитическими линейными представлениями связной односвязной комплексной группы Ли и вещественно аналитич. редставлениями ее связной вещественной формы G, при к-ром неприводимым представлениям соответствуют неприводимые. Это соответствие устанавливается следующим образом: если р - (неприводимое) конечномерное комплексно аналитическое представление группы G_C, то ограничение р на Gявляется (неприводимым) вещественно аналитич. редставлением группы G.

Не всякая вещественная группа Ли обладает комплексификацией. В частности, связная полупростая группа Ли Gобладает комплексификацией тогда и только тогда, когда Gлинейна, т. е. изоморфна подгруппе некоторой группы GL(n, С). Например, универсальная накрывающая группы вещественных матриц второго порядка с определителем 1 не имеет комплексификации. Однако всякая компактная группа Ли комплексификацией обладает.

Отсутствие комплексификации у нек-рых вещественных групп Ли инспирировало введение более общего понятия - универсальной комплексификации вещественной группы Ли G. Здесь - комплексная группа Ли, т :- вещественно аналитич. омоморфизм такой, что для любой комплексной группы Ли Hи любого вещественно аналитич. омоморфизма существует единственный комплексно аналитич. омоморфизм для к-рого Универсальная К. г. Ли всегда существует и определена однозначно [3]. Однозначность означает, что если - другая универсальная К. г. Ли G, то существует единственный изоморфизм для к-рого В общем случае если же Gодносвязна, то =и ядро гомоморфизма т дискретно.

См. также Форма группы Ли.

Лит.:[1] Наймарк М. А., Теория представлений групп, М., 1976; [2] Желобенко Д. П., Компактные группы Ли и их представления, М., 1970; [3] Бурбаки Н., Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 1976.

В. Л. Попов.