Akademik

- линейное представление топологич. группы в конечномерном векторном пространстве. Теория К. п. является одним из наиболее разработанных и важных разделов общей теории представлений групп. Неприводимое К. п. вполне неприводимо (см. Шура лемма), но операторно неприводимое К. п. может быть приводимым. Измеримое К. п. локально компактной группы совпадает локально почти всюду с нек-рым непрерывным К. п. Ограниченное К. п. локально компактной группы эквивалентно унитарному представлению. Локально компактная группа, имеющая точное К. п., является группой Ли [7].

Унитарное К. п. есть прямая сумма неприводимых унитарных К. п. Пересечение ядер непрерывных гомоморфизмов топологич. группы Gсовпадает с пересечением ядер неприводимых унитарных К. п. группы G; если это множество содержит лишь единичный элемент группы G, то группа Gдопускает непрерывный мономорфизм в нек-рую компактную группу и группа Gназ. вложимой в компактную группу, или максимальной почти периодической (МПП-группой). Если G- МПП-группа, то семейство матричных элементов неприводимых унитарных К. п. группы Gразделяет точки группы G. Коммутативные и компактные группы являются МПП-группами; связная локально компактная группа тогда и только тогда является МПП-группой, когда она есть прямое произведение связной компактной группы и группы Rⁿ (см. [5]). МПП-групгга может иметь бесконечномерные неприводимые унитарные представления и даже быть группой не типа 1. Для того чтобы любое непрерывное неприводимое унитарное представление локально компактной группы Gбыло К. п., необходимо и достаточно [8], чтобы группа Gявлялась проективным пределом конечных расширений групп Нвида где К, D, V- замкнутые подгруппы группы Н, причем группа Vизоморфна Rⁿ, К - компактная группа, D- дискретная группа, центральная в Н;достаточно, чтобы факторгруппа группы Gпо ее центру была компактна. Кроме того, для многих локально компактных групп (в частности, для некомпактных простых групп Ли) единственным неприводимым унитарным К. п. является единичное представление.

Неунитарные К. п. топологич. групп расклассифицированы (с точностью до эквивалентности) лишь для нек-рых групп, в частности для групп R и Z, где задача описания К. п. решается приведением матрицы к жордановой форме и - в случае группы R - связана с теорией обыкновенных дифференциальных уравнений с постоянными коэффициентами, так как пространство решений такого уравнения является конечномерным инвариантаым подпространством регулярного представления группы R в пространстве непрерывных функций на R. Кроме того, известны К. п. связных полупростых групп Ли. А именно, К. п. таких групп являются прямыми суммами неприводимых К. п., к-рые описываются следующим образом. Если G- полупростая комплексная группа Ли, U- ее максимальная компактная подгруппа, то любое непрерывное неприводимое унитарное представление p группы Uв пространстве Еможет быть продолжено: 1) до неприводимого представления p^G группы Gв Е, матричные элементы к-рого являются аналптич. функциями на G;2) до неприводимого представления прупцы p^G группы G, матричные элементы к-рого комплексно сопряжены аналитич. функциями на G;представления p^G и p^G определяются представлением я однозначно. Тензорное произведение является неприводимым К. п. группы Gдля любых неприводимых унитарных К. п. p₁, p₂ группы G, и любое неприводимое К. п. группы Gэквивалентно одному из представлений вида Описание К. п. односвязной связной комдлексной полупростой группы Ли может быть дано также в терминах экспонент К. п. ее алгебры Ли, а также с помощью Гаусса разложения группы G:пусть а - такая непрерывная функция на G, что a(z_-dz₊) = a(d) для всех и пусть линейная оболочка Ф _a функций конечномерна; тогда формула [T_a(g₀)f](g)=f(gg₀), g,.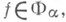определяет неприводимое К. п. группы G, и все неприводимые К. п. группы Gмогут быть получены таким образом. Если G - действительная полупростая группа Ли, имеющая комплексную форму то любое неприводимое К. п. группы Gявляется сужением на Gнек-рого однозначно определенного неприводимого К. п. группы 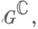матричные элементы к-рого аналитичны на (так что теория К. п. полупростых связных групп Ли по существу сводится к теории представлений компактных групп Ли). К. п. любой группы Ли является действительно аналитическим; если G- односвязная группа Ли, то между К. п. группы Gи ее алгебры Ли существует взаимно однозначное соответствие (сопоставляющее представлению группы Ли его дифференциал; обратное соответствие сопоставляет представлению алгебры Ли его экспоненту). Но классификация К. п. произвольных групп Ли далека (1978) от полного решения даже для частных случаев групп Rⁿ,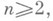как и для групп Zⁿ, (см. [6]). C другой стороны, неприводимые К. п. я связной группы Ли Gизвестны [2]: они имеют вид где c.- одномерное представление группы G(т. е. фактически - ее коммутативной факторгруппы по коммутанту), а p₀ - К. п. полупростой факторгруппы группы Gпо максимальному связному разрешимому нормальному делителю группы G(см. Леви- Мальцева разложение).

Лит.:[1] Кириллов А. А., Элементы теории представлений, М., 1972; [2] Желобенко Д. П., Компактные группы Ли и их представления, М., 1970; [3] Наймарк М. А., Теория представлений групп, М., 1976; [4] Диксмье Ж., С*-алгебры и их представления, пер. с франц., М., 1974; [5] Вейль А., Интегрирование в топологических группах и его применения, пер. с франц., М., 1950; [6] Гельфанд И. М., Пономарёв В. А., "Функциональный анализ и его применения", 1969, т. 3, №4, с. 81-82; [7] Глушков В. М., "Успехи матем. наук", 1957, т. 12, № 2, с. 3-41; [8] Штерн А. И., "Матем сб.", 1973, т. 90, № 1, с. 86-95.

А. И. Штерн.