Akademik

- дифференциально-геометрическая структура на гладком многообразии М, специальный вид связности на многообразии, когда приклеенное к Мгладкое расслоенное пространство Еимеет своим типовым слоем конформное пространство С _п размерности n=dim M. Структурой такого пространства Ек каждой точке присоединяется экземпляр конформного пространства ( С _п) _х, к-рый отождествляется (с точностью до конформных преобразований, сохраняющих х и все направления в ней) с касательным пространством Т _Х (М), дополненным одной бесконечно удаленной точкой. К. с, как связность в таком Е, предусматривает сопоставление каждой гладкой кривой 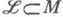с началом х ₀ и каждой ее точке x_t конформное отображение так, что удовлетворяется нек-рое условие (см. ниже условие на g_t). Пусть пространство СД отнесено к реперу, к-рый состоит из двух точек (вершин) и из нпроходящих через них попарно ортогональных гиперсфер. Такой репер интерпретируется в псевдоевклидовом пространстве ¹R_n+2 как класс эквивалентных базисов, удовлетворяющих условиям

относительно эквивалентности

Пусть Мпокрыто координатными областями и в каждой области фиксировано гладкое поле репера в ( С _п) _х, у к-рого вершина, определяемая вектором е ₀, совпадает с х. Условие на g_t следующее: при когда x_t перемещается по 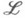до х ₀, g_t должно стремиться к тождественному отображению, причем главная часть его отклонения от последнего должна определяться относительно поля репера в нек-рой окрестности точки х ₀ матрицей вида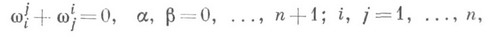

из 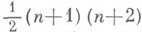линейных дифференциальных форм 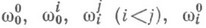типа

Другими словами, образ репера в точке x_t при g_t должен быть определен векторами

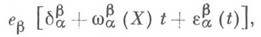
где X- касательный вектор к Lв точке х ₀ и

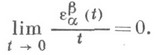
При преобразовании репера поля в произвольной точке хсогласно формулам сохраняющим условия (1), т. е. при переходе к произ-

вольному элементу главного расслоенного пространства П реперов в пространствах ( С _п) _х, формы (3) заменяются следующими 1-формами на П:

образующими также матрицу w' вида (2). 2-формы

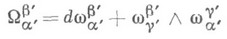
образуют матрицу такой же структуры, как (2), и выражаются по формулам через формы 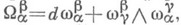являющиеся в силу (3) линейными комбинациями от 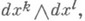а следовательно и от 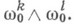Для элементов матрицы w' имеют место структурные уравнения К. с. (где для простоты опущены штрихи):

Здесь правые части полубазовы, т. е. являются линейными комбинациями только от 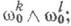они составляют систему форм кручения-кривизны К. с. и преобразуются по законам

Равенства имеют инвариантный смысл и выделяют К. с. нулевого кручения. Пусть

тогда при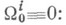

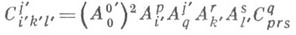
и для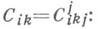

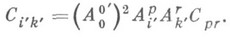
Инвариантные тождества C_ik=0 выделяет специальный класс так называемых (по Картану) нормальных К. с.

Формы (3), образующие матрицу вида (2), определяют К. с. на Моднозначно: образ репера в точке х _t при определяется решением {е_a(t)} системы

при начальных условиях и _a(0)=е_a, где xⁱ = xⁱ(t)-уравнения кривой 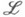в нек-рой координатной окрестности ее точки х ₀ с координатами х ⁱ(0). Любые 1-формы на П, удовлетворяющие уравнениям (4) с правыми частями, выражающимися через где (i=l, . . ., п)- линейно независимы, определяют в указанном смысле нек-рую К. с. на М. К. с. дают удобный аппарат для исследования конформных отображений римановых пространств. К. с. сводится к Леви-Чивита связности нек-рого риманова пространства, если на Мсуществуют локальные поля реперов, относительно к-рых

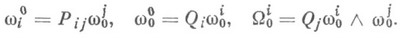
Для тензора кривизны R^j_ikl этой связности, определяемого равенством

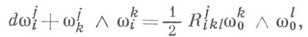
имеет место

Обратно, для каждой связности Леви-Чивита риманова пространства существует единственная нормальная К. с, из к-рой она получается указанным способом. При этом Q_j=0 п P_ij выражается через тензор Риччи R_ik=R^j_ikl и скалярную кривизну формулой

Соответствующий тензор C^j_ikl наз. тензором конформной кривизны связности Леви-Чивита. Два римановых пространства конформно эквивалентны, если их связности Леви-Чивита имеют совпадающие нормальные К. с. В частности, риманово пространство при n>3 конформно евклидово тогда и только тогда, когда для него c ^j_ikl=0.

Лит.:[1] Сartan E., "Ann. polon. math.", 1923, t. 2, s. 171-221; [2] Картан Э., Пространства аффинной, проективной и конформной связности, пер. с франц., Казань, 1962; [3] Оgiue К., "Kodai Math. Semin. Repts", 1967, v. 19, p. 193-224.

Ю. Г. Лумисте.