Akademik

численные методы решения - методы, заменяющие исходную краевую задачу дискретной задачей, содержащей конечное число N неизвестных, нахождение к-рых с соответствующей точностью позволяет определить решение исходной задачи с заданной точностью зависит от и стремится к при

Л. у. в случае dпространственных переменных имеет вид

и является однородным уравнением Пуассона. Краевые задачи для уравнения Лапласа являются частными случаями краевых задач для уравнения Пуассона и более общих уравнений эллиптич. типа (см. [1]), а численные методы решения краевых задач для уравнений эллиптич. типа (см. [2]) содержат в себе многие численные методы для уравнения Лапласа. Специфика Л. у. позволяет конструировать и использовать методы, обладающие существенно лучшими характеристиками, чем методы для более общих уравнений, хотя на практике часто этим возможностям предпочитают простоту реализации метода на ЭВМ.

Основными численными методами для уравнений эллиптич. типа являются: вариационно-разностные методы (проекционно-разностные, методы конечных элементов) и разностные методы (методы сеток). Оба класса методов связаны с аппроксимацией исходной области нек-рой сеточной областью содержащей Nузлов сетки, и построением системы алгебраич. уравнений

относительно значений функции, определяемой в этих узлах. В вариационно-разностных методах, являющихся специальными случаями вариационных и проекционных методов, используется идея аппроксимации рассматриваемого пространства функций, содержащего решение исходной задачи, нек-рыми специальными конечномерными подпространствами с заданными базисными функциями, а в системе (*) вектор состоит из коэффициентов разложения получаемой аппроксимации искомого решения по выбранному базису. В предположении, что решение исходной задачи в ограниченной области W на плоскости имеет вид

где - пространство Соболева, а функции заданы и отражают асимптотич. поведение и(х).вблизи особых точек (угловых точек границы, точек перемены типа граничного условия), для многих типов областей и смешанных краевых задач эти методы позволяют, напр., найти решение u(х).с точностью e в при затрате арифметич. действий (см. [3]), а в ряде более частных случаев оценки вычислительной работы уменьшаются до

В разностных методах обычно используется в той или иной форме аппроксимация производных разностями, и в системе (*) вектор состоит из компонент, апплоксимирующих значения решения в узлах сетки Наиболее изучены характеристики упомянутых методов для краевых задач в ограниченных областях W на плоскости. Напр., для условия Дирихле где Г - граница W и j(s) - достаточно гладкие, можно на основе улучшения дифференциальных свойств решения Л. у. по мере удаления от Г так построить систему (*), что число Nпо порядку равно числу N _Г точек на Г, используемых для задания j(s) с точностью e, а u_N может быть найдено с точностьюe при затрате арифметич. действий и дает возможность найти решение исходной задачи с точностью e в любой фиксированной точке из строго внутренней подобласти при затрате конечного числа действий (см. [4]). Методы такого типа являются асимптотически оптимальными; в случае же использования, напр., более простых методов с прямоугольной сеткой, обладающих точностью затраты на нахождение и _N с точностью e составляют 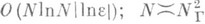(см. [4]). Наиболее детально изучены оценки погрешности метода сеток для Л. у. (см. [4], [5]); при наличии особых точек на Г целесообразно использовать специальную структуру сеток вблизи этих точек (см. [6]). Часто используются и разностные методы, основанные на аппроксимации нек-рых интегральных характеристик для Л. у. (см. [7] - [9]).

Относительно редко применяется метод коллокаций, в к-ром система (*) получается как следствие выполнения исходного уравнения в узлах сетки и предположения, что приближение к решению исходной задачи ищется в нек-ром конечномерном подпространстве. Специальный класс численных методов решения краевых зад-ач для Л. у. основан на сведении этих задач к сингулярным интегральным уравнениям (см. [1]) и последующему решению полученных интегральных уравнений численными методами (см. [10], [11]).

Лит.:[1] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [2] М а р ч у к Г. И., Методы вычислительной математики, 2 изд., М., 1980; [3] Дьяконов Е. Г., в сб.: Вариационно-разностные методы в математической физике, Новосиб., 1978, с. 149-64; [4] Б а х в а л о в Н. С., в сб.: Международный конгресс математиков в Ницце. 1970, М., 1972, с. 27-33; [5] Волков Е. А., "Ж. вычислит. матем. и матем. физики", 1969, т. 9, № 3, с. 573-84; [6] е г о же "Тр. матем. ин-та АН СССР", 1979, т. 150, с. 67-98; [7] Л ю с т е р н и к Л. А.."Успехи матем. наук", 1954, т. 9, в. 2, с. 3-66; [8] Самарский А. А., Ф р я з и н о в И. В., "Успехи матем. наук", 1976, т. 31, в. 6, с. 167-97; [9] Волков Е. А., "Докл. АН СССР", 1978, т. 238, Л" 5, с. 1036-39; [10] Партон В. 3., П е р л и н Б. И., Интегральные уравнения теории упругости, М., 1977; [11] Иванов В. В., в сб.: Механика сплошной среды и родственные проблемы анализа, М., 1972, с. 209-19. Е. Г. Дьяконов.