Akademik

полунепрерывный метод суммирования числовых и функциональных рядов, определенный последовательностью функций

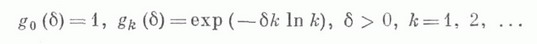
Ряд

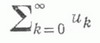
суммируем методом суммирования Линделёфа к сумме s, если

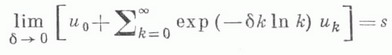
и ряд под знаком предела сходится. Метод был введен Э. Линделёфом [1] для суммирования степенных рядов. Л. м. с. является регулярным (см. Регулярные методы суммирования).и применяется как аппарат для аналитич. родолжения функций. Если f(z) - главная ветвь аналитич. функции, регулярной в нуле и представимой рядом

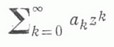
для малых z, то этот ряд суммируем Л. м. с. к f(z) во всей звезде функции f(z), причем равномерно во всякой замкнутой ограниченной области, содержащейся внутри звезды.

Из методов суммирования, определенных преобразованием последовательности в последовательность полунепрерывными матрицами 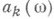типа

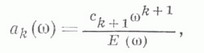
где

- целая функция, Э. Линделёфом рассматривался случай, когда

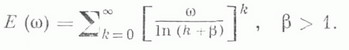
Матрицу 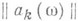с такой целой функцией иаз. м а т р и ц е й Л и н д е л ё ф а.

Лит.:[1] L i n d е 1 o f Е., "J. math.", 1903, t. 9, p. 213- 221; [2] его ж е, Le calcul des residue et ses applications a la theorie des fonctions, P., 1905; [3] Xapди Г., Расходящиеся ряды, пер. с англ., М., 1951; [4] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960.