Akademik

категорий - понятие, аналогичное понятию многообразия универсальных алгебр. Пусть 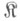- бикатегория с произведениями. Полная подкатегория категории 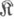наз. многообразием, если она удовлетворяет следующим условиям: а) если 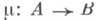- допустимый мономорфизм и б) если 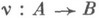- допустимый 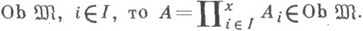эпиморфизм и 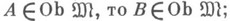в) если .

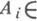Если бикатегория 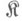локально мала слева, т. е. допустимые подобъекты любого объекта образуют множество, то всякое М. является рефлективной подкатегорией категории 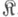. Это значит, что функтор вложения обладает сопряженным слева функтором 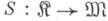. Единица этого сопряжения - естественное преобразование 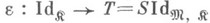обладает тем свойством, что для каждого 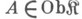морфизм является допустимым эпиморфизмом. Во многих важных случаях функтор Токазывается точным справа, т. е. он переводит коядро 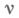пары мор-физмов в коядро пары морфизмов 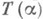, , 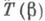если 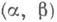- ядерная пара морфизма v. Более того, точность справа и наличие естественного преобразования являются характеристич. свойствами функтора Т.

Всякое М. наследует многие свойства объемлющей категории. Оно снабжается структурой бикатегории и является биполной категорией, если исходная категория биполна.

В категориях с нормальными кообразами, как и в случае многообразий групп, можно определить произведение М. Строение возникающего при этом группоида М. изучено только в ряде частных случаев.

Лит.:[1] Цаленко М. Ш., Шульгейфер Е. Г., Основы теории категорий, М., 1974; [2] Frohliсh A., "Quart. J. Math.", 1960, v. 11, № 43, p. 211-28.

M. Ш. Цаленпо.