Akademik

- группа, допускающая эндоморфизм на себя с нетривиальным ядром, т. е. изоморфная пек-рой своей собственной факторгруппе (в противном случае группа наз. хопфовой). Термин происходит от проблемы Xопфа (Н. Hopf, 1932) о существовании таких групп с конечным множеством порождающих. Оказалось, что существуют даже конечно определенные Н. г. Примером конечно порожденной Н. г. является группа с порождающими х, у и одним определяющим соотношением

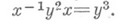
Бесконечно порожденные Н. г. строятся совсем просто, таково, напр., прямое произведение бесконечного числа изоморфных между собой групп.

Лит.:[1] Курош А. Г., Теория групп, 3 изд., М., 1967; [2] Магнус В., Каррас А., Солитэр Д., Комбинаторная теория групп, пер. с англ., М., 1974.

А. Л. Шмелькин