Akademik

детерминант, квадратной матрицы А=||a_ij|| порядка пнад ассоциативно-коммутативным кольцом K с единицей 1 - элемент кольца K, равный сумме всех членов вида

где i₁, . . ., i_n- перестановка чисел 1, . . ., п,a t- число инверсий перестановки i₁,..., i_n. О. матрицы обозначается

О. матрицы Асодержит п! членов; при n-1 det A =a₁₁, при п=2det А=а ₁₁ а ₂₂-a_2la₁₂. Наиболее важные для приложений случаи: K - поле (в частности, числовое поле), К - кольцо функций (в частности, кольцо многочленов), K - кольцо целых чисел.

Всюду ниже К- ассоциативно-коммутативное кольцо с 1, М _п (К) - совокупность всех квадратных матриц порядка пнад K, Е _п- единичная матрица над А. Пусть , а а ₁, . . ., а _п- строки матрицы А(все далее изложенное справедливо и для столбцов матрицы А). О. матрицы A удобно рассматривать как функцию от ее строк:

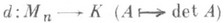
Отображение

подчинено следующим трем условиям:

1) d(A) - линейная функция любой строки матрицы А:

где l, ;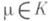

2) если матрица Вполучена из Азаметной строки а _i строкой , , 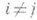то ;

3)

Условия 1) - 3) однозначно определяют отображение d, т. е. если отображение удовлетворяет условиям 1) - 3), то h(A)=detА. Таким образом получается аксиоматич. построение теории О.

Пусть отображение удовлетворяет условию:

1 _а) если Вполучается из матрицы Л умножением одной строки на 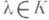,то 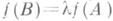. Очевидно, В случае, когда К- поле, совокупность условий 1) - 3) оказывается равносильной условиям 1 _а), 2), 3).

О. диагональной матрицы равен произведению ее диагональных элементов. Отсюда вытекает сюръективность отображения . О. треугольной матрицы также равен произведению ее диагональных

элементов. Для матрицы 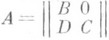, где Ви С- квадратные матрицы,

Из свойств перестановок вытекает, что > где ^Т - знак транспонирования. Если матрица Аимеет две одинаковые строки, то ее определитель равен 0; если поменять местами две строки матрицы А, то ее О. изменит знак;

при ; для А и В из М _п (К)

Таким образом, отображение dесть эпиморфизм мультипликативных полугрупп М _п (К).и K.

Пусть есть (mx n) матрица, есть (nx m) - матрица над K, а С=АВ. Тогда верна формула Вине-Коши:

Пусть , a A_ij- алгебраич. дополнение элемента a_ij. Тогда верны формулы

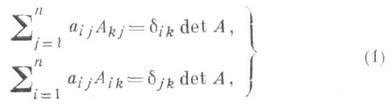
где - символ Кронекера. Для вычислений О. часто используются разложение его по элементам строки или столбца, т. е. формулы (1), теорема Лапласа (см. Алгебраическое дополнение).и преобразования матрицы А, не меняющие О. Для матрицы Аиз М _п (К).тогда и только тогда существует обратная матрица А ^-1 в М _п (К), когда в Кимеется элемент, обратный элементу del A . Следовательно, отображение

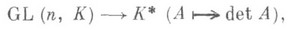
где GL ( п, К) - группа всех обратимых матриц в М _п (К), т. е. полная линейная группа, а К*- группа обратимых элементов K, есть эпиморфизм этих групп. Квадратная матрица над полем обратима тогда и только тогда, когда ее О. отличен от нуля, n-мервые векторы a₁..., а _п над полем Fлинейно зависимы тогда и только тогда, когда

О. матрицы Апорядка n>1 над полем равен 1 тогда и только тогда, когда Аесть произведение элементарных матриц вида

где , a e_ij - матрица, единственный ненулевой элемент к-рой равен 1 и расположен на позиции (i, j). Теория О. возникла в связи с задачей решения систем линейных уравнений:

где a_ij, b_j- элементы нек-рого поля F. Если , где 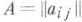- матрица системы (2), то эта система имеет единственное решение, вычисляемое по формулам Крамера (см. Крамера правило). В случае, когда система (2) задана над кольцом Ки det Аобратим в К, система также имеет единственное решение, определяемое теми же формулами Крамера.

Теория О. построена также и для матриц над некоммутативным ассоциативным телом. О. матрицы над телом k(определитель Дьёдонне) вводится следующим образом. Тело kрассматривается как полугруппа и строится ее коммутативный гомоморфный образ . k - группа k* с внешне присоединенным нулем 0, а в качестве берется также группа с внешне присоединенным нулем , где - факторгруппа группы k* по коммутанту. Эпиморфизм задается канонич. эпиморфизмом групп и условием . Очевидно, - единица полугруппы

Теория О. над телом основана на следующей теореме. Существует единственное отображение

удовлетворяющее следующим трем аксиомам:

I) если матрица Вполучена из матрицы Аумножением слева одной строки на 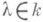, то ;

II) если Вполучена из Азаменой строки a_i строкой a_i+a_j, где , то ;

III)

Элемент наз. определителем матрицы Аи обозначается det A. Для коммутативного тела аксиомы I), II), III) совпадают с условиями 1 _а), 2), 3) соответственно, и, следовательно, в этом случае получаются обычные О. над полем. Если A = diag [a_n,...,а _ап], то таким образом, отображение сюръективно. Матрица Аиз M_n(k).обратима тогда и только тогда, когда . Справедливо равенство . Как и в коммутативном случае, det Ане изменится, если строку а _i матрицы Азаменить строкой , где При тогда и только тогда, когда Апроизведение элементарных матриц вида , . Если , то

В отличие от коммутативного случая, det A^T может и не совпадать с det А. Напр., для матрицы

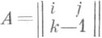
над телом кватернионов, а

Бесконечные О., то есть О. бесконечных матриц, определяются как предел, к к-рому стремится О. конечной подматрицы при бесконечном возрастании ее порядка. Если этот предел существует, то О. наз. сходящимся, в противном случае - расходящимся.

Понятие "О." восходит к Г. Лейбницу (G. Leibnitz, 1678); первая публикация принадлежит Г. Крамеру (G. Cramer, 1750). Теория О. создана трудами А. Ван-дермонда (A. Vandermonde), П. Лапласа (P. Laplace), О. Коши (A. Cauchy) и К. Якоби (С. Jacobi). Термин "О." встречается впервые у К. Гаусса (С. Gauss, 1801). Современное обозначение введено А. Кэли (A. Cayley, 1841).

Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975; [2] Кострикин А. И., Введение в алгебру, М., 1977; [3] Ефимов Н. В., Розендорн Э. Р., Линейная алгебра и многомерная геометрия, М., 1970; L4] Тышкевич Р. И., Феденко А. С., Линейная алгебра и аналитическая геометрия, 2 изд., Минск, 1976;[5] А р т и н Э., Геометрическая алгебра, пер. с англ., М., 1969; М Б у р б а к и Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [7] Каган В. Ф., Основания теории определителей, Одесса, 1922. Д. А. Супруненко.