термин, используемый в теории оптимального управления для описания оптимального способа управления системой в случае, когда минимизирующая последовательность управляющих функций не имеет предела в классе измеримых по Лебегу функций.
Пусть, напр., требуется найти минимум функционала
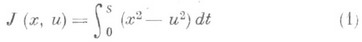
при условиях
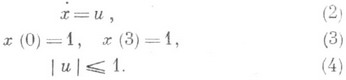
Для получения минимума функционала (1) желательно иметь при каждом tкак можно меньшее значение |x(t)|и как можно большее значение |u(t)|. Первому требованию, с учетом условия связи (2), граничных условий (3) и ограничений на управление (4), удовлетворяет траектория
Если бы траекторию (5) можно было построить при иек-ром управлении, принимающем при всех tграничные значения
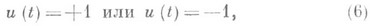
был бы получен абсолютный минимум функционала (1), Однако "идеальная" траектория (5) не может быть построена ни при какой управляющей функции u(t), удовлетворяющей (6), поскольку при 
Тем не менее можно, используя управляющие функции u п(t), реализующие при 
и 1<t<2 все более частые переключения с 1 на -1 и обратно:
построить минимизирующую последовательность управлений {un(t)}, удовлетворяющую (6), и минимизирующую последовательность траекторий {xn(t)},cxoдящуюcя к "идеальной" траектории (5).
Каждая из траекторий xn(t). отличается от (5) только на интервале (1, 2), на к-ром в. место точного движения по оси хона обеспечивает "пилообразное" движение с n одинаковыми "зубьями", расположенными над осью х."Зубья пилы" становятся все мельче при 
, так что , l<t<2. Таким образом, минимизирующая 
последовательность траекторий {xn(t)}сходится к (5), но минимизирующая последовательность управлений {un(t)}, реализующих при 
и 1<t<2 все более частые переключения с 1 на -1 и обратно, не имеет предела в классе измеримых (а тем более в классе кусочно непрерывных) функций. Это означает, что на участке (1, 2) имеет место О. р. с.
Используя не очень строгие рассуждения, можно описать полученный О. р. с. следующим образом: оптимальное управление в каждой точке интервала (1, 2) "скользит", т. е. перескакивает со значения +1 на -1 и обратно так, что для любого, сколь угодно малого, интервала времени мера множества точек t, в к-рых u=+1, равна мере множества точек t, в к-рых и=-1, что обеспечивает, в силу уравнения (2), точное движение по оси х. Приведенное описание характера изменения оптимального управления на участке скользящего режима является нестрогим, ибо оно не удовлетворяет обычному определению функции.
Можно дать строгое определение О. р. с., если наряду с исходной задачей (1)-(4) ввести в рассмотрение вспомогательную, расщепленную задачу: найти минимум функционала
при условиях
Расщепленная задача (8)-(11) отличается от исходной тем, что: вместо одной управляющей функции u(t).вводятся две независимые управляющие функции u0(t).и u1(t);подинтегральная функция и функция, стоящая в правой части уравнения (2) исходной задачи, заменяются линейной выпуклой комбинацией соответствующих функций, взятых при различных управлениях u0(t).и u1(t).с коэффициентами a0(t), a1(t), к-рые также рассматриваются как управляющие функции.
Таким образом, в задаче (8)-(11) имеется 4 управления u0, u1, a0, a1. Поскольку a0 и a1 связаны условием типа равенства ac+a1=l, то от одного из управлений a0 или a1 можно избавиться, выразив его через другое. Однако для удобства последующего анализа целесообразно оставить оба эти управления в явном виде.
В отличие от исходной задачи оптимальное управление в расщепленной задаче (8)-(11) существует. На участке О. р. с. исходной задачи оптимальное управление расщепленной задачи имеет вид
а на участках входа и выхода
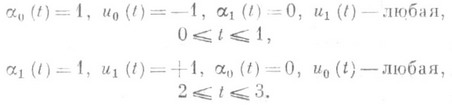
На участке О. р. с. управления a0 и a1, линейно входящие в правую часть и подинтегральную функцию, принимают значения, лежащие внутри допустимой области. Это означает, что О. р. с. исходной задачи (1) - (4) есть особый оптимальный режим, или особое оптимальное управление, для вспомогательной, расщепленной задачи (8)-(11).
Аналогичные результаты для О. р. с. имеют место в общем случае задачи оптимального управления. Пусть требуется найти минимум функционала
(12)
При условиях
О. р. с. характеризуется неединственностью максимума по ифункции Гамильтона
где yi- - сопряженные переменные (см. [2]). При этом на участке [t1, t2] "скольжения" по k+1, k>1, максимумам u0, и 1, ... , uk исходная задача расщепляется и принимает вид
Функцию Гамильтона для задачи (16)-(19)
после исключения a0 и перегруппировки слагаемых можно привести к виду
Поскольку все H(t, x, y, us),s=0, 1, ... , k, есть равные между собой максимумы Hпо ина множестве U, то на участке [t1, t2] О. р. с. с k+1 максимумами коэффициенты при k независимых линейных управлениях a1..., ak функции Гамильтона расщепленной задачи (12)-(15) равны нулю. О. р. с. со "скольжением" по k+1 максимумам есть особый оптимальный режим по kкомпонентам для расщепленной задачи (16)-(19). Максимально возможное значение k, к-рое целесообразно брать при исследовании скользящих режимов, определяется из условия выпуклости множества значений вектора правых частей и выпуклости вниз точной нижней границы множества значений подинтегральной функции расщепленной системы, получающихся, когда вектор управления (as, us), s=0,1,...,kпробегает всю допустимую область значений. Таким образом, 
- оценка сверху для k. В самом общем случае все О. р. с. исходной задачи могут быть получены как особые оптимальные управления расщепленной задачи, записанной при k=n. В частности, в рассмотренном выше примере расщепленная задача рассматривалась при k=1, поскольку условия связи содержали только одно уравнение; исследование расщепленной задачи (8)-(11) было достаточно для исследования О. р. с. исходной задачи (1)-(4).
Если известны k+1 управлений u0(t),и 1(t),...,uk(t), доставляющих равные между собой абсолютные максимумы функции Гамильтона H(t, x,y, и).в допустимой области U, то анализ О. р. с. сводится к исследованию особого оптимального режима по kкомпонентам. Это исследование может быть проведено с использованием необходимых условий оптимальности особого управления (см. Оптимальный режим особый).
Исследовались О. р. с. с помощью достаточных условий оптимальности (см. [4]).
Лит.:[1] Гамкрелидзе Р. В., "Докл. АН СССР", 1962, т. 143, № 6, с. 1243 - 45; [2] IIонтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф., Математическая теория оптимальных процессов, 2 изд., М., 1969; [3] Вапнярский И. Б., "Ж. вычислит, матем. и матем. физ.", 1967, т. 7, № 2, с.259-83; [4] Кротов В. Ф., "Автоматика и телемеханика", 1963, т. 24, № 5, с. 581-98.
И. Б. Вапнярский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.