Akademik

свойство траектории x (решения х(t)) автономной системы обыкновенных дифференциальных уравнений

состоящее в следующем: для всякого e>0 существует d>0 такое, что всякая положительная полутраектория, начинающаяся в d-окрестности траектории x, содержится в e-окрестности траектории x. Здесь под траекторией понимается множество значений решения x(t),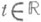, системы (*), а под положительной полутраекторией - множество значений решения x(t).при . Если решение x(t).устойчиво по Ляпунову, то его траектория орбитально устойчива.

Траектория x наз. асимптотически орбитально устойчивой, если она орбитально устойчива и, кроме того, найдется d₀>0 такое, что траектория всякого решения x(t).системы (*), начинающегося в d₀ -окрестности траектории x (т. е. d(x(0), x)<d₀), стремится при к траектории x, то есть

где

- расстояние от точки хдо множества x (d(x, у) - расстояние между точками хи у).

Роль понятия асимптотической орбитальной устойчивости основана на следующих фактах. Периодич. решение системы (*) никогда не бывает асимптотически устойчивым. Но если у периодич. решения такой системы модули всех мультипликаторов, кроме одного, меньше единицы, то траектория этого периодич. решения асимптотически орбитально устойчива (Андронова - Витта теорема).

Имеет место также более общая теорема Демидов и ча (см. [3]): пусть x₀(t) - ограниченное решение системы (*), причем

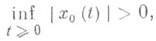
и пусть система уравнений в вариациях вдоль x₀(t).- правильная (см. Правильная линейная система), причем все ее Ляпунова характеристические показатели, кроме одного, отрицательны; тогда траектория решения x₀(t).асимптотически орбитально устойчива.

Лит.: [1] Андронов А. А., Собр. трудов, М., 1956; [2] Андропов А. А., Витт А. А., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959; [3] Демидович Б. П., "Дифференц. уравнения", 1968, т. 4, № 4, с. 575-88; № 8, с. 1359-73.

В. М. Миллионщиков.