Akademik

- обобщенный стационарный случайный процесс с постоянной спектральной плотностью. Корреляционная (обобщенная) функция процесса Б. ш. имеет вид: - нек-рая положительная постоянная, а -дельта-функция. Процесс Б. ш. широко используется в приложениях для описания случайных возмущений с очень малым временем корреляции (напр., "теплового шума" - пульсаций силы тока в проводнике, вызываемых тепловым движением электронов). В спектральном разложении Б. ш.

"элементарные колебания" при всех частотах имеют в среднем одинаковую интенсивность, точнее, их средний квадрат амплитуды есть

Указанное выше спектральное разложение означает, что для любой интегрируемой с квадратом функции

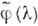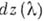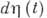где - преобразование Фурье ; более явная зависимость обобщенного процесса от функции может быть описана с помощью соответствующей стохастич. меры того же типа, что и ( - преобразование Фурье стохастич. меры ), а именно

Гауссовскпй белый шум , являющийся обобщенной производной от броуновского движения , служит основой для построения стохастических диффузионных процессов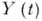,"управляемых" стохастическими дифференциальными уравнениями вида

эти уравнения обычно записывают в форме дифференциалов:

Другой важной моделью с использованием Б. ш. является случайный процесс , описывающий поведение устойчивой колебательной системы под воздействием стационарных случайных возмущений , когда не зависят от простейшим примером может служить система вида

где - многочлен с корнями в левой полуплоскости; после затухания "переходных процессов"

В приложениях, при описании так наз. процессов дробового эффекта, большую роль играет Б. ш. вида

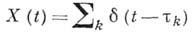
(k изменяется от - случайные моменты, распределенные во времени по пуас-соновскому закону), точнее, является обобщенной производной пуассоновского процесса h(t).Сам процесс дробового эффекта имеет вид:

где - нек-рая весовая функция, удовлетворяющая условию

при этом среднее значение обобщенного процесса есть

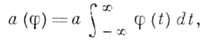
где а - параметр упомянутого выше пуассоновского закона, и стохастич. мера в спектральном представлении

этого процесса такова, что

Лит.:[1] Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, М., 1967. Ю. А. Розанов.