Akademik

множества - взаимно однозначное отображение множества на себя. Термин "П." главным образом применяется для конечного множества X. В этом случае удобно считать, что Х={1, . . ., п}, изаписывать П. в виде

(*)

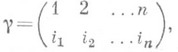где i₁, i₂, . . ., i_n - нек-рая перестановка чисел 1, 2, . . ., n (впрочем, иногда термин "перестановка" употребляется как синоним термина "П.", см., напр., [2] с. 146). Запись (*) означает, что gпереводит число kв i_k, то есть y(k)=i_k (пишут также kg=i_k).для i=1, 2, . . ., n. Число всех различных П. множества Xпри |Х| = n равно числу всех перестановок этого множества, т. е. n!. Произведение подстановок a и b множества 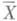определяется как последовательное выполнение отображений a и b и задается формулой ab(x)=a(b(x)) для всех 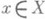. Совокупность всех П. множества Xобразует группу относительно введенного умножения, к-рая наз. симметрической группой. Любая подгруппа симметрич. группы наз. подстановок группой.

Симметрич. группа П. множества Xобозначается S(X), она содержит в качестве подгруппы SF(X) - группу, состоящую из таких подстановок g, к-рые перемещают лишь конечное подмножество элементов (то есть 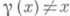лишь для конечного множества элементов 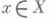). Если Xконечно и состоит из пэлементов, то симметрич. группа обозначается S_n.

Транспозицией наз. такая П. множества X, к-рая меняет местами только два элемента iи j; она обозначается (i, j). В S _п имеется ровно ( п-1)/2 транспозиций. Любая подстановка g. из SF(X).представима в виде произведения транспозиций. В частности, каждая П. из S_n есть произведение транспозиций. П. может разлагаться в произведение транспозиций многими способами. Однако для данной g. характер четности числа множителей в разложении на транспозиции не зависит от способа разложения. П., представимая в виде произведения четного числа транспозиций, наз. четной, а разлагающаяся в произведение нечетного числа транспозиций - нечетной. В S_n имеется n!/2 четных П. и столько же нечетных. Если П. 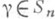записана в виде (*), то ее четность совпадает с четностью числа инверсий перестановки i₁, . . ., i_n к-рое равно числу таких пар {i_k, i_j}, что k<j, i_k>i_j. Транспозиция, очевидно, есть нечетная II. Применение одной транспозиции к любой перестановке меняет четность числа ее инверсий на противоположную. Произведение двух четных, а также двух нечетных П. ость четная П., а четной и нечетной П. (в любом порядке) - нечетная. Все четные П. составляют нормальную подгруппу (X).в группе SF(X), к-рая наз. знакопеременной. При |Х|= п подгруппа (X).обозначается А _п.

Циклом длины lназ. такая подстановка а конечного множества Y={y₁, . . ., у _l], что

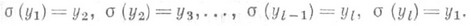
Конечный цикл обозначается (y₁, y₂, . . ., y_l). Бесконечным циклом наз. такая П. счетного множества

что для любого целого i s(y_i)=y_i+1 Обозначение бесконечного цикла таково:

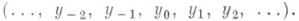
Цикл длины 2 есть транспозиция. Группа S_n содержит ( п-1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид

где g^l(x}=x, а бесконечные -

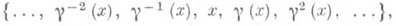
где 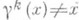при 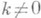. Циклы, индуцируемые подстановкой Y на подмножествах разбиения, наз. независимыми циклами подстановки g. Например, (1, 3, 4) и (2, 5)- независимые циклы П.

g записывается в виде

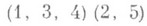
и является произведением своих независимых циклов. Вообще, если g нетождественная П., имеющая лишь конечное число циклов неединичной длины, то g - произведение таких циклов. В частности, каждая нетождественная П. из SF(X).является произведением своих независимых циклов неединичной длины. Порядок подстановки g из SF(X), т. е. порядок циклич. группы <g>, равен наименьшему общему кратному длин ее независимых циклов.

Из независимых циклов данной П. можно получить независимые циклы П., сопряженной с ней. Напр., если

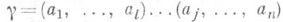
произведение независимых циклов подстановки g из S_n, а и d( а _i)=b_i, i=l, . . ., п, то

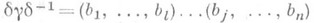
- разложение подстановки 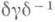в произведение независимых циклов. Две П. группы S_n тогда и только тогда сопряжены в S_n, когда они имеют одно и то же число независимых циклов каждой длины.

Пусть , k - число независимых циклов подстановки s, включая и циклы длины 1. Тогда разность п-kназ. декрементом подстановки s. Наименьшее число множителей при разложении подстановки s в произведение транспозиций совпадает с ее декрементом. Четность П. совпадает с четностью ее декремента.

П. возникли впервые в комбинаторике 18 в. В кон. 18 в. Ж. Лагранж (J. Lagrange) применил их при исследовании разрешимости алгебраич. уравнении в радикалах. О. Коши (A. Cauchy) посвятил многочисленные исследования этому понятию. Ему, в частности, принадлежит идея разложения П. в произведение циклов. Исследования групповых свойств П. восходит к Н. Абелю (N. Abel) и особенно к Э. Галуа (Е. Galois). См. Галуа теория, Подстановок группа.

Лит.:[1] Jordan С., Traite des substitutions et des equations altfebriques, P., 1057; [2] Кострикин А. И., Введение в алгебру, М., 1977; [3] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975; [4] Холл М., Теория групп, пер. с англ., М., 1962. Д. А. Супруненко.