Akademik

- решение и ( х, а). x=(x₁, . . ., х _n), a=(a₁ . . ., a_n), дифференциального уравнения с частными производными 1-го порядка

(1)

к-рое зависит от ппараметров a₁, . . ., а _n и в рассматриваемой области удовлетворяет условию

Если и( х, а).рассматривать как n-параметрическое семейство решений, то огибающая любого его ( п-1)-параметрического подсемейства, выделяемого условием

является решением уравнения (1). При этом линии касания поверхностей, задаваемых полным интегралом, и огибающей являются характеристиками (1). С помощью П. и. можно описать решения характеристич. системы обыкновенных дифференциальных уравнений, отвечающей уравнению (1), и, следовательно, обратить метод Коши, к-рый сводит решение уравнения (1) к решению характеристич. системы. Этот подход применяется в аналитич. механике, где требуется найти решение канонич. системы обыкновенных дифференциальных уравнений

(2)

Эта система является характеристической для уравнения Я коби

(3)

Если для уравнения (3) П. и. u=u(x₁, . . . , х _n, t. a_l ,.... a_n)+a₀ известен, то 2n интегралов канонич. системы (2) даются равенствами ,

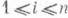, где a_i,b_i - произвольные постоянные.

А. П. Солдатов.