тела Архимеда,- выпуклые многогранники, все грани к-рых суть правильные многоугольники, а многогранные углы конгруэнтны или симметричны. Данные о П. м. приведены в таблице, где В - число вершин, Р - число ребер, Г - число граней, Г k. - число nk- угольных граней, s - число граней, сходящихся в каждой вершине, в том числе s1 n1 -угольных, s2 n2 -уголышх и т. д. В евклидовом пространстве R3 существует 13 П. м. [см. рис., 1-14, иногда выделяют два вида ромбокубооктаэдра (рис., 3-4), к-рые различаются тем, что верхняя часть многоугольника, состоящая из 5 квадратов и 4 правильных треугольников, повернута как целое на угол p/4] и две бесконечные серии - призмы (рис., 15 )и антипризмы (рис., 16).
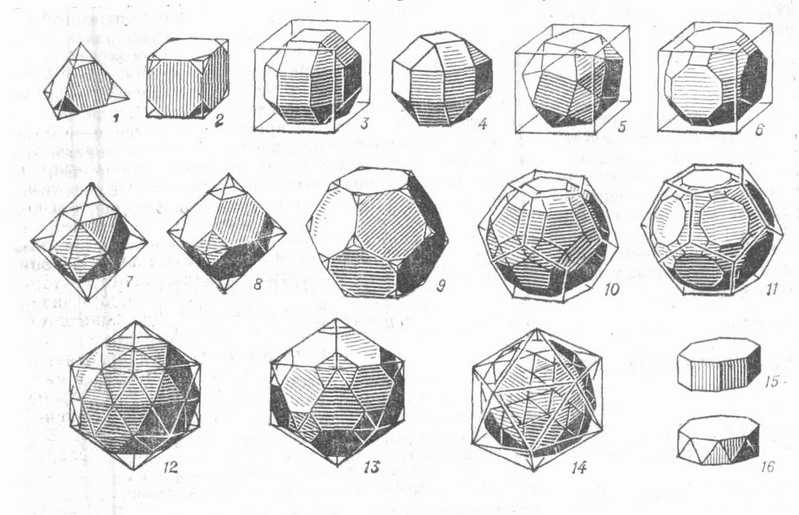
Полуправильные многогранники
| | № на рис. | В | P | Г | п 1 | n2 | n3 | Г 1 | Г 2 | Г 3 | s1 | s2 | s3 | s | ||
| Усеченный тетраэдр | 1 | 12 | 18 | 8 | 6 | 3 | - | 4 | 4 | - | 2 | 1 | - | 3 | ||
| Усеченный куб | 2 | 24 | 36 | 14 | 8 | 3 | - | 6 | 8 | - | 2 | 1 | - | 3 | ||
| Ромбокубооктаэдр | 3, 4 | 24 | 48 | 26 | 4 | 3 | - | 18 | 8 | - | 3 | 1 | - | 4 | ||
| Плосконосый куб | 5 | 24 | 60 | 38 | 3 | 4 | - | 32 | 6 | - | 4 | 1 | - | 5 | ||
| Усеченный кубооктаэдр | 6 | 48 | 72 | 26 | 4 | 6 | 8 | 12 | 8 | 6 | 1 | 1 | 1 | 3 | ||
| Кубооктаэдр | 7 | 12 | 24 | 14 | 3 | 4 | - | 8 | 6 | - | 2 | 2 | - | 4 | ||
| Усеченный октаэдр | 8 | 24 | 36 | 14 | 6 | 4 | - | 8 | 6 | - | 2 | 1 | - | 3 | ||
| Усеченный додекаэдр | 9 | 60 | 90 | 32 | 10 | 3 | - | 12 | 20 | - | 2 | 1 | - | 3 | ||
| Ромбоикосододекаэдр | 10 | 60 | 120 | 62 | 4 | 3 | 5 | 30 | 20 | 12 | 2 | 1 | 1 | 4 | ||
| Усеченный икосододекаэдр | 11 | 120 | 180 | 62 | 4 | 6 | 10 | 30 | 20 | 12 | 1 | 1 | 1 | 3 | ||
| Икосододекаэдр | 12 | 30 | 60 | 32 | 3 | 5 | - | 20 | 12 | - | 2 | 2 | - | 4 | ||
| Усеченный икосаэдр | 13 | 60 | 90 | 32 | 6 | 5 | - | 20 | 12 | - | 2 | 1 | - | 3 | ||
| Плосконосый додекаэдр | 14 | 60 | 150 | 92 | 3 | 5 | - | 80 | 12 | - | 4 | 1 | - | 5 | ||
| Правильная призма (n = 3, 5, 6,...) | I5 | 2n | Зn | n + 2 | 4 | n | - | п | 2 | - | 2 | 1 | - | 3 | ||
| Антипризма (n = 4, 5, 6,...) | 16 | 2п | 4n | 2n + 2 | 3 | n | - | 2n | 2 | - | 3 | 1 | - | 4 | ||
Невыпуклых (звездчатых) П. м. больше 51.
Лит.:[1] Энциклопедия элементарной математики, кн. 4- Геометрия, М.-Л., 1963; [2] Люстерник Л. А., Выпуклые фигуры и многогранники, М., 1956; [3] Bruckner M., Vielecke und Vielflache. Theorie.. und Geschichtc, Lpz., 1900: [4] Веннинджер М., Модели многогранников, пер. с англ., М., 1974. А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.