Akademik

- понятие гомотопич. топологии; инвариант, равный нулю, если соответствующая задача разрешима, и отличный от нуля - в противном случае.

Пусть (X, А) - пара клеточных пространств и У - односвязное (более общо - гомотопически простое) топологич. пространство. Можно ли данное непрерывное отображение продолжить до непрерывного отображения Продолжение можно осуществлять по остовам Х ^п пространства X. Пусть построено такое отображение , что f|_A = g. Для любой ориентированной (n+1)-мерной клетки 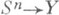отображение 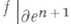задает отоб ражение (где Sⁿ есть n-мерная сфера) и элемент 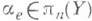(именно здесь и используется гомотопич. простота пространства Y, позволяющая игнорировать выбор отмеченной точки). Таким образом, возникает коцепь

Так как для 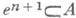, очевидно, , то на самом деле

Очевидно, 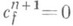тогда и только тогда, когда f продолжается на Х ⁿ⁺¹, т. е. коцепь является препятствием к продолжению f на Х ^{п + 1}.

Коцепь является коциклом. Ил того, что , вообще говоря, не следует, что gне продолжается на X: f может не продолжаться на Х ^п+1 в силу неудачного выбора продолжения gна Xⁿ. Может оказаться, напр., что отображение продолжается на Х ^{п + 1}, т. е. что продолжение возможно после отступления на один шаг. Оказывается, что П. 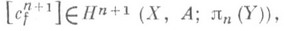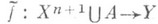к этому является класс когомологий то есть тогда и только тогда, когда существует такое отображение , что (в частности, 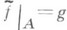). Для доказательства этого утверждения используется конструкция различающей.

Так как задачу гомотопич. классификации отображений можно интерпретировать как задачу продолжения, то теория П. применима и к описанию множества [X, Y]гомотопич. классов отображений из X в Y. Пусть I=[0, 1] и пусть - подпространство в . Тогда пара отображений f₀, f₁, : XY интерпретируется как отображение G: А Y, G(x, i)=f_i(x), i=0, 1, и наличие гомотопии между f₀ и f₁ означает наличие отображения F: XX IY, продолжающего отображение G. При этом если гомотопия Fпостроена на re-мерном остове пространства X, то П. к ее продолжению на Xесть различающая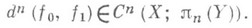

В качестве приложения можно указать описание множества [X, Y]=[X, K(p, n)], n>1, где K(p, п) - Эйленберга - Маклейна пространство:p_i(K(p,n))=0 при 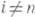, p_n(K(p, n))=p. Пусть 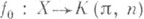- постоянное отображение, а - произвольное непрерывное отображение. Так как Н ⁱ (Х;p_i (Y)) = 0 при i<n, то f₀ и f₁ гомотопны на Х ^п-1 и можно, выбрав какую-нибудь такую гомотопию, определить различающую

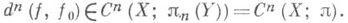
Класс когомологий 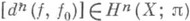определен корректно, т. е. не зависит от выбора гомотопии между f₀ и f (в силу того, что p_i(Y)=0 при i<n). Далее, если отображения таковы, что [dⁿ(f, f₀)]=[dⁿ(f, f₀)], то [dⁿ(f,g)]=0 и, значит, f и gгомотопны на Xⁿ. П. к продолжению этой гомотопии на все Xлежат в группах Н ⁱ (Х;p_i(Y))=0 (так как i>n), и, значит, отображения f и g гомотопны. Таким образом, гомотопич. класс отображения f полностью определяется элементом . Наконец, для любого элемента найдется отображение f с [dⁿ(f,f₀)]=x и потому [X, K(p,п)]= Н ⁿ (Х;p). Аналогично: если p_i(Y)=i при i<n и dim X п, то [ Х, У] =Hⁿ (Х;p_n(Y)).

При исследовании задачи продолжения рассматривалась возможность продолжения после "отступления на один шаг". Полное решение задачи требует анализа возможности продолжения после отступления на произвольное число шагов. Для этой цели используются когомологические операции или Постникова системы. Так, для описания множества [X, Y], где p_i(Y)=0 при 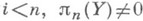, dim X=n+r, требуется, вообще говоря, исследовать возможность отступления на r+1 шаг, для чего надо исследовать первые n+r этажей системы Постникова пространства Y, т. е. использовать когомологич. операции порядков r(в ст. Когомологические операции эта задача разобрана для r=1).

Теория П. используется также в более общей ситуации продолжения сечений. Пусть 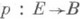- нек-рое расслоение со слоем F(причем p₁(F)=0 и p₁ (В) действует на p₁(F).тривиально), пусть и 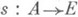- нек-рое сечение (т. е. такое непрерывное отображение, что ps(a)=a). Можно ли продолжить sна все В? Соответствующие П. лежат в группах Н ^п+1 (В;p_n(F)). Задача продолжения получается из этой задачи, если положить В=Х,, р( х, y)=x,s(a)=(a,g(a)). Аналогичным образом с помощью теории П. исследуется и задача классификации сечений.

Наконец, в задаче продолжения можно снять ограничение гомотопич. простоты пространства Y (и аналогично в задаче о сечениях); для этого надо использовать когомологий с локальными коэффициентами.

Ю. Б. Рудяк.