Akademik

многочлен , где R - ассоциативно-коммутативное кольцо с однозначным разложением на множители, коэффициенты к-рого не имеют нетривиальных общих делителей. Любой многочлен 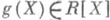можно записать в виде g(X)=c(g)f(X), где f(X) - П. м., a c(g) -наибольший общий делитель коэффициентов многочлена g(X). Элемент 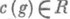, определенный с точностью до умножения на обратимые элементы из R, наз. содержанием многочлена g(X). Справедлива лемма Гаусса: если , то с(g₁g₂)=c(g₁)c(g₂). В частности, произведение П. м. снова примитивно.

Лит.:[1] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963. Л. В. Кузьмин.