Akademik

алгебры Л и Sс ядром А - алгебра Ли G с эпиморфизмом , ядром к-рого служит идеал AМG, это равносильно заданию точной последовательности

Р. наз. р а с щ е п и м ы м, если существует подалгебра SМS такая, что (прямая сумма модулей). Тогда j индуцирует изоморфизм , и потому определено действие алгебры Sна Адифференцированиями. Обратно, по любому гомоморфизму , где Der A - алгебра дифференцирований алгебры А, однозначно строится расщепимое расширение с законом умножения

Для конечномерных алгебр Ли над полем характеристики 0 справедлива т е о р е м а Л е в и: если Sполупроста, то всякое расширение алгебры Sрасщепимо. Из нерасщепимых Р. наиболее изучены абелевы Р., то есть Р. с абелевым ядром А. В этом случае действие алгебры G на Аиндуцирует действие алгебры 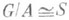на А, то есть Аесть S-модуль. Для алгебр Ли над полем всякое абелево Р. алгебры S, ядром к-рого служит S-модуль А, имеет вид со следующим законом умножения:

где - нек-рое линейное отображение Тождество Якоби равносильно тому, что - двумерный коцикл (см. Когомологии алгебр Ли). Р., к-рым эквивалентны когомологичные коциклы, эквивалентны в естественном смысле; в частности, Р. расщепимо тогда и только тогда, когда когомологичен нулю. Таким образом, абелевы Р. алгебры Sсядром Аописываются группой когомологий H²(S, А). К случаю абелевых Р. сводится изучение Р. с разрешимым ядром.

Лит.:[1] Д ж е к о б с о н Н., Алгебры Ли, пер. с англ., М., 1964. А. К. Толпыго.