Akademik

- число, выражаемое рациональной дробью. Формальная теория Р. ч. строится с помощью пар целых чисел. Р а ц и о н а л ь н о й д р о б ь ю 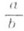наз. упорядоченная пара ( а, b )целых чисел а и b, у к-рой b№0. Две рациональные дроб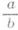и и наз. э к в и в а л е н т н ы м и (р а в н ы м и) тогда и только тогда, когда ad=bc. Это соотношение эквивалентности, будучи рефлексивно, симметрично и транзитивно, разбивает множество всех рациональных дробей на классы эквивалентности. Р а ц и он а л ь н ы м ч и с л о м наз. каждый класс эквивалентности рациональных дробей. Разные классы определяют разные Р. ч. Множество Р. ч. счетно. Р. ч., содержащее рациональную дробь вида 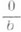, наз. н у л е м. Если r есть Р. ч. и 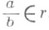, то Р. ч., содержащее рациональную дробь , наз. рациональным числом, противоположным Р. ч. r, и обозначается через - r. Р. ч. r наз. п о л о ж и т е л ь н ы м (о т р и ц а т е л ьн ы м), если оно содержит рациональную дробь 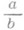, у к-рой аи dодного знака (разных знаков). Если Р. ч. положительно (отрицательно), то противоположное ему число отрицательно (положительно). В множестве Р. ч. вводится упорядоченность: всякое отрицательное Р. ч. считается меньшим всякого положительного, положительное Р. ч. r' считается меньшим положительного Р. ч. , если существуют такие рациональные дроби , что ad<bc;всякое отрицательное (положительное) Р. ч. r считается меньше (больше) нуля: r<0 (r>0); отрицательное Р. ч. r' считается меньшим отрицательного Р. ч. , если положительное Р. ч.-- r' больше положительного Р. ч.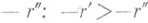. Абсолютная величина Р. ч. определяется как обычно:, если , если r<0.

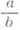Суммой рациональных дробей и наз. рациональная дробь , а произведением . С у мм о й и п р о и з в е д е н и е м Р. ч. r' и r" наз. классы эквивалентных рациональных дробей, содержащие соответственно сумму или произведение рациональных дробей и , принадлежащих r' и r":

.

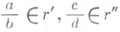Упорядоченность, сумма и произведение Р. ч. r' и r" не зависят от выбора представителей в соответствующих классах эквивалентности и , т. е. однозначно определяются самими Р. ч. r' и r". Р. ч. образуют упорядоченное поле, обозначаемое ;

Для обозначения Р. ч. rприменяются рациональные дроби ия класса эквивалентности, задающего это число:

. Таким образом, одно и то же Р. ч. может быть записано разными, но эквивалентными рациональными дробями.

Если каждому Р. ч., содержащему рациональную дробь вида 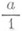, поставить в соответствие целое число а, то получится изоморфное отображение множества указанных Р. ч. на кольцо целых чисел. Поэтому

Р. ч., содержащие рациональные дроби вида , обозначают через а.

Всякая функция вида

(1)

является метрикой в поле Р. ч. , то есть удовлетворяет условиям:

при любых 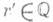и . Поле Р. ч. не является полным в метрике (1). Пополнением поля Р. ч. по метрике (1) является поле действительных чисел. Функция

(2) где р - простое число, r-Р. ч., представимое в виде

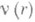( - целое, - несократимая рациональная дробь, причем числа аи bне делятся на p), а r - фиксированное число, 0<r<1, также является метрикой в поле Р. ч. . Она наз. р-а д и ч е с к о й м е т р и к о й. Поле Р. ч. с метрикой (2) не является полным. Пополнением поля Р. ч. по метрике (2) является поле р-адических чисел. Метрики (1) и (2) (для всех простых чисел) исчерпывают все нетривиальные метрики в поле Р. ч.

В десятичной записи Р. ч. и только они представимы периодическими десятичными дробями.

Лит.:[1] Б о р е в и ч 3. И., III а ф а р е в и ч И. Р., Теория чисел, 2 изд., М., 1972; [2] II и з о Ш., 3 а м а н с к и й М., Курс математики. Алгебра и анализ, пер. с франц., М., 1971.

Л. Д. Кудрявцев.