Akademik

уточнение интуиционистской семантики арифметич. суждений на основе понятия частично рекурсивной функции, предложенное С. Клини (см. [1], [2]). Для всякой замкнутой арифметич. формулы Fопределяется отношение "натуральное число ереализует формулу F", обозначаемое erF. Отношение erF определяется индуктивно в соответствии с построением формулы F.

1) Если F - элементарная формула без свободных переменных, т. е. формула вида s=t, где s и t - постоянные термы, то erF тогда и только тогда, когда е=0 и значения термов s и tсовпадают.

Пусть Аи В - формулы без свободных переменных.

2) тогда и только тогда, когда , где аrА, brВ.

3) тогда и только тогда, когда и аrА или е=2^1.3^b и brВ.

4) еr (АЙВ)тогда и только тогда, когда е - гёделев номер такой одноместной частично рекурсивной функции j, что для любого натурального числа а, если аrА, то j применима к aи j(а)rВ.

5) тогда и только тогда, когда er(AЙ1=0).

Пусть А(х)- формула без свободных переменных, отличных от х;если п - натуральное число, то - терм, изображающий в формальной арифметике число n.

6) 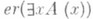тогда и только тогда, когда е = 2^n.3^a и .

7) тогда и только тогда, когда е- гёделев номер такой общерекурсивной функции f, что для любого натурального пчисло f(n)реализует

Замкнутая формула Fназывается р е а л и з у е м о й, если существует число е, реализующее F. Формула А(y₁,. . .,y_m), содержащая свободные переменные y₁,. . ., у _m, может рассматриваться как предикат от y₁, ..., y _т("формула A (у ₁,. .., у _т )реализуема"). Если формула Fвыводима из реализуемых формул в интуиционистском арифметическом исчислении, то Fреализуема (см. [3]). В частности, всякая формула, доказуемая в интуиционистской арифметике, реализуема.

Можно указать такую формулу А(х), что формула не реализуема. Соответственно, в этом случае формула 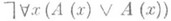реализуема, хотя является классически ложной.

Всякая предикатная формула , доказуемая в интуиционистском исчислении предикатов, обладает тем свойством, что каждая арифметич. формула, получающаяся из 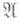подстановкой, реализуема. Предикатные формулы, обладающие этим свойством, наз. р е а л из у е м ы м и. Было показано [4], что пропозициональная формула

где Dобозначает формулу , реализуема, но не выводима в интуиционистском исчислении высказываний.

Лит.:[1] К 1 е е n e S. С., "J. Symbolic Logic", 1945, v. 10, p. 109-24; [2] К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] N e l s o n D., "Trans. Amer. Math. Soc.", 1947, v. 61, p. 307-68; [4] R о s e G. F., там же, 1953, v. 75, p. 1 -19; [5] H о в и к о в П. С., Конструктивная математическая логика с точки зрения классической, М., 1977.

В. Е. Плиско.