Akademik

, ослабления м е т о д,- метод итерационного решения системы линейных алгебраич. уравнений Ах=b, элементарный шаг к-рого состоит в изменении только одной компоненты вектора неизвестных, причем номера изменяемых компонент выбираются в нек-ром циклич. порядке. Наиболее часто Р. м. используется для решения систем с положительно определенной матрицей А.

Если изменение одной компоненты вектора неизвестных осуществляется так, что для нового приближения 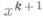квадратичная форма минимизируется, то Р. м. наз. м е т о д о м п о л н о й р е л а к с а ц и и. Если же за один элементарный шаг значение квадратичной формы лишь уменьшается, но не минимизируется, то Р. м. наз. м е т о д о м н е п о лн о й р е л а к с а ц и и .

Наиболее полно исследован м е т о д п о с л е д ов а т е л ь н о й в е р х н е й р е л а к с а ц и и, когда матрица Аобладает т. н. свойством (А) и согласованно упорядочена. Матрица Аназ. матрицей, обладающей с в о й с т в о м (А), если существует матрица перестановок Ртакая, что матрица РАР ^Т имеет форму

, где D₁ и D₂ - квадратные диагональные матрицы .

Итерационная схема P.м. имеет следующий вид:

где w - параметр релаксации, D - диагональная, L - нижняя треугольная и U - верхняя треугольная матрицы из разложения A=D+L+U. Если w>1, то метод наз. м е т о д о м в е р х н е й р е л а к с а ц и и (с в е р х р е л а к с а ц и и), если -м е т о д о м н и ж н е й р е л а к с а ц и и. Параметр w выбирается из условия минимизации спектрального радиуса матрицы Sперехода от итерации к итерации:

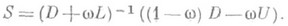
Если А - симметричная матрица с положительными диагональными элементами и l_i- корни детерминантного уравнения 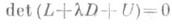, то оптимальное значение параметра w дается формулой

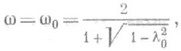
где Для w= w₀ спектральный радиус матрицы S равен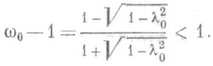

Рассмотрены случаи, когда нек-рые l_i комплексны. Разработаны методы блочной релаксации.

Лит.:[1] Y о u n g D. M., "Trans. Amer. Math. Soc.", 1954, v. 76, № 1, p. 92-111; [2] е г о ж е, Iterative solution of large linear systems, N. Y.-L., 1971; [3] В а з о в В., Ф о рс а й т Дж., Разностные методы решения дифференциальных уравнений в частных производных, пер. с англ., М., 1963; [4] Ф а д д е е в Д. К., Ф а д д е е в а В. Н., Вычислительные методы линейной алгебры, М., 1960. Е. С. Николаев.