Akademik

- статистический критерий, применяемый для проверки простой непараметрич. гипотезы Н ₀, согласно к-рой независимые одинаково распределенные случайные величины X₁, ... , X_n имеют заданную непрерывную функцию распределения F(x), против

альтернатив следующего вида:

где - функция эмпирич. распределения, построенная по выборке - весовая функция. В случае, если

где а - любое фиксированное число из отрезка [0, 1], то Р. к., предназначенный для проверки H₀ против указанных альтернатив 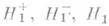, основан на соответствующих им с т а т и с т и к а х Р е н ь и:

где Х ₍₁₎, Х ₍₂₎ ... , Х _(n) - члены вариационного ряда

построенного по наблюдениям X₁, ..., Х _(n).

Статистики и подчиняются одному и тому же вероятностному закону, и если , то

(1)

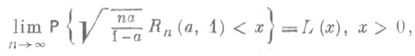(2)

где Ф (х) - функция распределения стандартного нормального закона, L(х) - ф у н к ц и я р а с п р е д е л е н и я Р е н ь и, определяемая формулой:

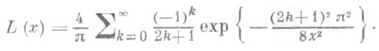
В случае, если a=0, то

Из (1) и (2) следует, что при больших значениях nдля вычисления Q-процентных критич. значений 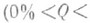для статистик и можно воспользоваться следующими приближенными значениями:

соответственно, где и функции, обратные Ф (х)и L(х)соответственно, при этом имеют в виду, что если 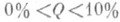, то

Кроме того, если x>2,99, то при вычислении значений функции распределения Реньи L(х)рекомендуется пользоваться приближенным равенством

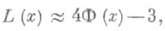
погрешность к-рого не превосходит 5^.10^-7.

Кроме рассмотренных Р. к., существуют аналогичные критерии, отвечающие весовой функций

где а- любое фиксированное число из отрезка [0, 1]. Лит.:[1] R e n у i A., "Acta math. Acad. scient. hung.", 1953, v. 4, p. 191- 231; [2] Г а е к Я., Ш и д а к 3., Теория ранговых критериев, пер. с англ., М., 1971; [3] Б о л ь ш е в Л. Н., С м и р н о в Н. В., Таблицы математической статистики, 2 изд., М., 1968. М. С. Никулин.