дифференциального уравнения
(*)
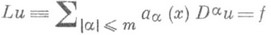в области D - это локально интегрируемая функция и, к-рая имеет локально интегрируемые обобщенные производные всех порядков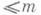 
и удовлетворяет уравнению (*) почти всюду в области D.
Понятие "С. р." может быть введено и таким образом. Функция иназ. С. р. уравнения (*), если существуют такие последовательности гладких (напр., класса 
) функций {un}, {fn}, что 
и 
при каждом n, где сходимость понимается в L1(K)для любого компакта 
. В этих определениях L1 можно заменить классом Lp локально интегрируемых со степенью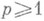 
функций. Наиболее употребительным является класс L2.
В случае эллиптич. уравнения (*) оба понятия
С. р. совпадают. А. П . Солдатов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.