Akademik

1) С. д. в узком смысле слова - исследование определяемого ниже топологич. автоморфизма Бернулли s - его инвариантных замкнутых подмножеств, инвариантных мер и т. д. Топологический а в т о м о р ф и з м Бернулли s действует в пространстве W бесконечных двусторонних последовательностей символов из нек-рого алфавита А (обычно конечного), снабженном топологией прямого произведения бесконечного числа экземпляров А(в каждом из к-рых обычно берется дискретная топология). А именно, s. переводит последовательность w={w_i} в 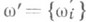, где ("сдвиг последовательности на один шаг налево"). Очевидное обобщение - действие группы (или полугруппы) Gв пространстве А ^G.

Пусть нек-рые пары ( а, b )символов из Аобъявлены "допустимыми". Всевозможные последовательности {w_i}, для к-рых при всех i пары (w_i, w_i+1) допустимы, образуют нек-рое замкнутое инвариантное (относительно s) подмножество . Это - важнейший пример инвариантного подмножества топологич. автоморфизма Бернулли. Динамич. система в W₁, порожденная сдвигом , наз. топологической цепью Маркова.

2) С. д. в широком смысле слова - применение С. д. в узком смысле слова к исследованию динамич. систем, к-рые сами по себе определяются совершенно независимо от W и s.

Лит.:[1] А л е к с е е в В. М., Символическая динамика, К., 1976 (Одиннадцатая [летняя] математическая школа, ч. 1); [2] Б о у э н Р., Методы символической динамики, пер. с англ., М., 1979 (Новое в зарубежной науке. Математика, в. 13).

Д. В. Аносов.