Akademik

с и м м е т р и з а ц и я,- одна из операций тензорной алгебры, при помощи к-рой но данному тензору строится симметричный (по группе индексов) тензор. С. всегда производится над несколькими верхними или нижними индексами. Тензор S с координатами 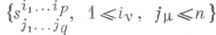является результатом С. тензора Тс координатами , 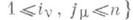по тверхним индексам, напр. по группе индексов I= (i₁, i₂, . . ., i_m), если

(*)

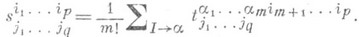Здесь суммирование производится по всем т!перестановкам a=(a₁, a₂, . . ., a _т )группы индексов I. С. по группе нижних индексов определяется аналогично. С. по группе индексов обозначается взятием этих индексов в круглые скобки ( ). Посторонние индексы (не участвующие в С.) отделяются вертикальными черточками. Напр.,

Последовательное С. по группам индексов I₁ и I₂, , совпадает с С. по группе индексов I₂. Другими словами, если то 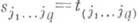(внутренние скобки снимаются).

Тензор, не изменяющийся при С. по нек-рой группе индексов, наз. симметрическим тензором.

С. по нек-рой группе индексов тензора, альтернированного (см. Альтернирование )по этой группе, дает нулевой тензор.

Умножение двух и более тензоров с последующим С. их произведения по всем индексам наз. симметрическим умножением. С. тензоров, наряду с операцией альтернирования, применяется для разложения тензора на тензоры более простого строения. С. применяется также для образования сумм вида (*) с многоиндексными слагаемыми. Напр., если элементы матрицы

/

коммутируют при умножении, то выражение

наз. п е р м а н е н т о м м а т р и ц ы.

Лит.:[1] Ш и р о к о в П. А., Тензорное исчисление, 2 изд., Казань, 1961; [2] Б е к л е м и ш е в Д. В., Курс аналитической геометрии и линейной алгебры, М., 1971; [3] С х о у т е н Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965.

Л. П. Купцов.