Akademik

обобщение понятия производной на случай функций множества Ф в n-мерном евклидовом пространстве. С. п. в точке хесть предел

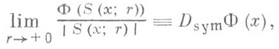
где S(х; r) - замкнутый шар с центром в точке хи радиусом r. С. п. порядка nв точке хфункции действительного переменного f(х).наз. предел

Функция действительного переменного f(х).имеет С. п. в точке хпорядка 2r:

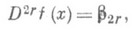
если

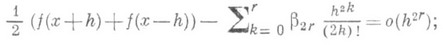
порядка 2r+1:

если

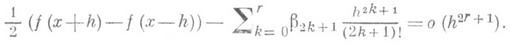
Если в точке хсуществует п-я производная f⁽ⁿ⁾ (х), то в этой точке существует (в обоих смыслах) С. п. и она равна f⁽ⁿ⁾ (х). Если f(х).имеет в точке хпроизводную D^2rf(x). или D^2r+1f(x), то она имеет производную Dⁿf(x). Обратное утверждение справедливо при условии существования всех производных Dⁿf(x).меньшего порядка той же четности.

Лит.:[1] Сакс С., Теория интеграла, пер. с англ., М., 1949; [2] James R. D., "Trans. Amer. Math. Soc.", 1954, v. 76, № 1, p. 149 - 76. Т. П. Лукашенко.