- термин, употребляемый в математич. статистике для названия функций от результатов наблюдении.
Пусть случайная величина Х принимает значения в выборочном пространстве  Тогда любое
Тогда любое  -измеримое отображение
-измеримое отображение  пространства
пространства  в некрое измеримое пространство
в некрое измеримое пространство 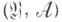 наз. статистикой, при этом распределение вероятностей статистики Топределяется формулой
наз. статистикой, при этом распределение вероятностей статистики Топределяется формулой

Примеры. 1. Пусть X1, . .., Х п- независимые одинаково распределенные случайные величины, имеющие дисперсию. Тогда С.

суть несмещенные оценки для математич. ожидания  и дисперсии
и дисперсии  соответственно.
соответственно.
2. Члены вариационного ряда

построенного по наблюдениям X1, . .., Х п суть порядковые статистики.
3. Пусть случайные величины X1, . .., Х п образуют стационарный случайный процесс, спектральная плотность к-рого есть  В этом случае С.
В этом случае С.

называемая периодограммой, при определенных условиях регулярности на  является асимптотически несмещенной оценкой для
является асимптотически несмещенной оценкой для  т. е.
т. е.

В теории оценивания и проверки статистич. гипотез важную роль играет понятие достаточной статистики, к-рая позволяет производить редукцию данных без потери информации об изучаемом параметрич. семействе распределений.
Лит.:[1] Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964.
М. С. Никулин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.