Akademik

функция 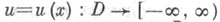точки х= (х ₁, . . ., х _п )евклидова пространства определенная в области 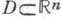и обладающая следующими свойствами: 1) и(х)полунепрерывна сверху в D;2) для любой точки 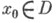существуют сколь угодно малые значения r>0 такие, что

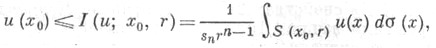
где I(и; х₀, r) - среднее значение функции и(х)по площади сферы S(х ₀, r )с центром х ₀ радиуса 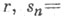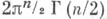- площадь единичной сферы в 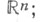3) 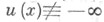(это условие иногда опускается). В данном определении С. ф. среднее значение I(и; х₀, r )поплощади сферы можно заменить на среднее значение

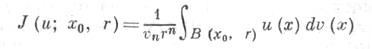
по объему шара В(х ₀, r), где v_n=s_n/n - объем единичного шара в
Равносильное определение С. ф., объясняющее название лС. ф.