Akademik

группа G, на к-рой может быть введено отношение линейного порядка такое, что влечет за собой для любых Группа G тогда и только тогда является У. г., когда в ней существует подмножество . со свойствами: 1)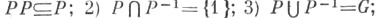 4) для любого
Пусть S(a₁, а ₂, ... , а _п) - нормальная подполугруппа группы G, порожденная элементами a₁, а ₂, ... , а _п. Группа G тогда и только тогда является У. г., когда для любого конечного набора a₁, ... , а _п элементов из G, отличных от единицы группы, найдется такой набор чисел равных что подполугруппа не содержит единицу. Всякая У. г. есть группа с однозначным извлечением корня. Абелевы группы без кручения, локально нильпотентные группы без кручения, свободные, свободные разрешимые группы суть У. г. Двуступенно разрешимая группа, для всякого неединичного элемента хк-рой является У. г.
Класс У. г. замкнут относительно подгрупп, фильтрованных произведений, локально замкнут и, следовательно, является квазимногообразием. Свободное произведение У. г. есть У. г.

Лит.:[1] Кокорин А. И., Копытов В. М., Линейно упорядоченные группы, М., 1972; [2] Фукс Л., Частично упорядоченные алгебраические системы, пер. с англ., М., 1965.
В. М. Копытов.