Akademik

- вариационный принцип, позволяющий находить лучи, т. е. кривые, вдоль к-рых распространяется волновой процесс. Пусть х=х₁, ..., х _т, 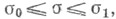- уравнение кривой l, соединяющей точки М ₀ и M₁, с=с(x)>0 - скорость распространения волн в точке х. Ф. п. утверждает, что для луча, соединяющего М ₀ и М ₁. Здесь - символ вариации, - дифференциал дуги. Физич. смысл -время движения из M₀ в M₁ вдоль . со скоростью с(х). Из Ф. п. следуют классич. законы отражения, преломления, прямолинейность лучей при с= const. Дифракционные лучи, лучи, распространяющиеся от краев экранов, лучи головных волн тоже можно найти, пользуясь Ф. п. Лучи, определяемые Ф. п., являются характеристиками эйконала уравнения. Интеграл 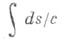задает риманову метрику частного типа. Лучи - геодезические, соответствующие этой метрике. Ф. п. обобщается на случай скорости, зависящей от направления (анизотропная среда). Лучи в этом случае - геодезические нек-рой финслеровой метрики.
Ф. п. для задачи преломления света был впервые высказан П. Ферма (P. Fermat, ок. 1660).

Лит. см. при ст. Лучевой метов.
В. М. Бабич.