Akademik

- подмножество Fоднородного пространства Е _п с фундаментальной группой G, к-рое можно включить в систему (F)подмножеств этого пространства, изоморфную нек-рому пространству геометрич. объекта Ф (см. Геометрических объектов теория).Множество R(F)наз. пространством фигуры F. Компоненты геометрич. объекта Ф наз. координатами соответствующей Ф. F. Каждой Ф. F пространства Е _п соответствует класс {Ф} подобных геометрич. объектов. Ранг, жанр, характеристика и тип геометрич. объекта Ф класса {Ф} наз. рангом,
жанром, характеристикой и типом фигуры F(т. н. арифметические инварианты фигуры). Напр., окружность в трехмерном евклидовом пространстве является фигурой ранга 6, жанра 1, характеристики 1, типа 1; точка в трехмерном проективном пространстве - фигурой ранга 3, жанра 0, характеристики 2, типа 1. Вполне интегрируемая система уравнений Пфаффа, определяющая геометрический объект Ф, наз. системой уравнений стационарностифигуры F.
Пусть Fи 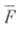-две Ф. пространства Е _п. Если существует отображение пространства R(F)на пространство 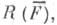при к-ром любой геометрич. объект, соответствующий Ф. 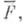охватывается любым геометрич. объектом, соответствующим Ф. F, то говорят, что Ф. Fохватывает или индуцирует 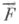Ф. (Ф. 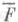охватывается или индуцируется Ф. F). Ф. Fранга Nназ. простой, если она не охватывает никакой другой Ф. меньшего ранга. Ф. . наз. индуцирующей фигурой индекса 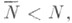если существует охватываемая ею Ф. ранга 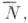причем ранг N' любой другой Ф. F', охватываемой Ф. F, не превосходит 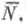Напр., точка, р-мерная плоскость, гиперквадрика в n-мерном проективном пространстве являются простыми Ф., а гиперквадрика в n-мерном аффинном пространстве и d-мерная 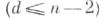квадрика в n-мерном проективном пространстве являются индуцирующими Ф. соответственно индексов n и (d+2)(n- d-1).
Парой фигур F=(F_l, F₂ )наз. упорядоченная совокупность двух Ф. Коэффициентом инцидентности пары Ф. наз. число k=N₁+N₂-N, где Ni(i=1,2) ранг фигуры F_i, а N - ранг системы форм 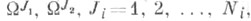являющихся левыми частями уравнений стационарности Ф. F₁ и F₂. Если k =0, то пара F =(F₁, F₂ )наз. неинцидентной.

Лит.:[1] Лаптев Г. Ф., лТр. Моск. матем. об-ва