Akademik

- раздел математического программирования, в к-ром исследуется задача оптимизации (максимизации пли минимизации) функции нескольких переменных, связанных рядом уравнений и (или) неравенств и удовлетворяющих условию целочисленности (используются также термины дискретное программирование, дискретная оптимизация). Источником задач Ц. п. является техническая, экономическая и военная проблематика.
Условие целочисленности переменных формально отражает: а) физич. неделимость объектов (напр., при размещении предприятий или выборе варианта боевых действий); б) конечность множества допустимых вариантов, на к-ром проводится оптимизация (напр., множества перестановок в задачах упорядочения); в) наличие логич. условий, выполнение или невыполнение к-рых влечет изменение вида целевой функции и ограничений задачи.
Наиболее изученной и распространенной задачей Ц. п. является т. н. задача целочисленного линейного программирования: максимизировать

при условиях

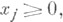j = 1, 2, . .., п, x_j - целые для j = 1, ..., р, где а _ij, b_i, c_j- заданные целые числа, x_j- переменные.
Методы решения задач Ц. п. (релаксация, отсечения, динамическое программирование, метод лветви и границы