Akademik

- плоская трансцендентная кривая; траектория точки окружности, катящейся по прямой линии (рис. 1).

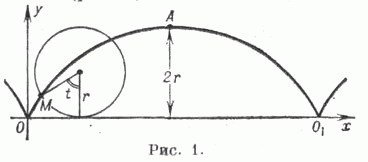
Параметрич. уравнения: x = rt - rsin t, y = r-rcos t, где r - радиус окружности, t- угол поворота окружности. Уравнение в декартовых прямоугольных координатах: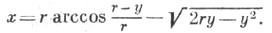

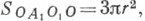Ц. - периодич. кривая: период (базис) OO₁ = 2pr. Точки -точки возврата. Точки - т. н. вершины. Площадь: радиус кривизны: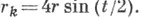
Если кривая описывается точкой, лежащей вне (внутри) окружности, к-рая катится по прямой, то она наз. удлиненной (рис. 2) (укороченной, рис. 3) циклоидой, или, иногда, трохоидой.

Параметрические уравнения: x = rt - d sin l, y = r-dcos l, где d - расстояние точки Мот центра катящейся окружности.
Ц. является таутохронной (или изохронной) кривой, т. е. такой, что время спуска материальной точки но этой кривой под действием силы тяжести до определенной высоты не зависит от исходного положения точки на кривой.

Д. Д. Соколов.