Akademik

- плоская кривая, описываемая точкой, к-рая связана с окружностью, катящийся по другой окружности.
Если производящая точка находится на окружности, то Ц. к. наз. эпициклоидой или гипоциклоидой в зависимости от того, расположена ли катящаяся окружность вне или внутри неподвижной окружности. Если же точка расположена вне или внутри катящейся окружности, то Ц. к. наз. трохоидой.
Вид Ц. к. зависит от соотношения между радиусами окружностей. Так, если отношение радиусов - число рациональное, то Ц. к. есть замкнутая алгебраич. кривая, если же это отношение - число иррациональное, то Ц. к. не замкнута. Среди эпициклоид наиболее известна кардиоида, среди гипоциклоид - астроида и Штейнера кривая.
Параметрич. уравнения Ц. к. можно записать в комплексном виде:
Это уравнение является частным случаем уравнения 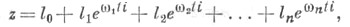описывающего циклоиды высших порядков.

Лит.:[1] Савелов А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.