Akademik

- способ записи интерполяционного многочлена, получающегося из Гаусса интерполяционной формулы для интерполирования вперед по узлам x₀, x₀+h, х ₀-h, . . ., x₀+nh, x₀-nh, x₀+(n+1)h в точке x=x₀+th

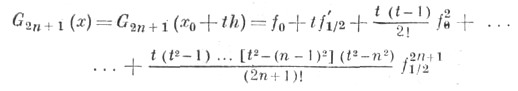
исключением конечных разностей нечетного порядка при помощи соотношения

После приведения подобных членов получается Э. и. ф.

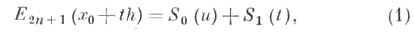
где u=1 - t,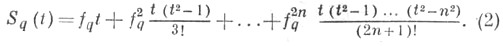

Формула [1] примерно вдвое сокращает работу по сравнению с другими записями интерполяционного многочлена при решении задачи уплотнения таблиц, т. е. когда из данной таблицы значений функции с узлами x₀+kh требуется составить таблицу значений функции с узлами x₀+kh' при h'=h/l, где l - целое, поскольку в этом случае значения f(x₀-th) при 0<t<1 вычисляются по формуле
f(x₀-th)= S₀(u) + S_₁(t);
значение S₀(u) используется при нахождении двух значений
При ручном счете в случае n = 2 коэффициент при в (2) целесообразно приблизить выражением

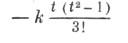
и вместо S_q(t)вычислять

Параметр kможно выбирать, напр., из условия минимума главной части величины

где

В этом случае значение k= 3,0785.

Лит.:[1] Бeрезин И. С., Жидков Н. П., Методы вычислений, а изд., т. 1, М., 1966; [2] Бахвалoв Н. С., Численные методы, 2 изд., М., 1975.
М. К. Самарин.