Akademik

(действительный) - плоская кривая, получающаяся в пересечении кругового конуса с плоскостью, не проходящей через вершину конуса и пересекающей все его образующие в точках одной его полости. Э. есть множество точек Мплоскости (см. рис.), для каждой из к-рых сумма расстояний до двух данных точек F₁ и F₂ (фокусов) постоянна и равна 2а>F₁F₂. Расстояние между фокусами наз. фокусным расстоянием, его принято обозначать через 2с. Середина отрезка F₁F₂ наз. центром Э.

Прямая, на к-рой лежат фокусы Э., наз. первой (или фокальной) осью. Прямая, проходящая через центр Э. перпендикулярно к первой оси, наз. второй осью Э. Оси Э. являются его осями симметрии. Точки пересечения Э. с осями симметрии наз. его вершинами. Большой осью Э. наз. отрезок (а также длина 2аэтого отрезка) первой оси Э., заключенный между вершинами Э. Малой осью Э. наз. отрезок (а также длина 2bэтого отрезка) второй оси Э., заключенного между вершинами Э. Число е=с/а<1 наз. эксцентриситетом Э. Диаметром Э. наз. любая прямая, проходящая через центр Э.; диаметр может быть определен как прямая, проходящая через середины параллельных хорд. Директрисой Э., соответствующей данному фокусу F, наз. прямая d, перпендикулярная первой оси Э. и отстоящая от центра Э. на расстоянии a/e. В общем случае у Э. имеются две директрисы. Э. есть центральная линия второго порядка, канонич. уравнение к-рой имеет вид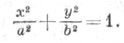

Уравнение касательной к Э. в точке (х ₀, у₀):

Фокальный параметр Э. (половина длины хорды, проходящей через фокус перпендикулярно первой оси Э.) равен b²/а. При помощи фокального параметра можно записать уравнение Э. в виде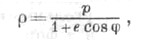

где - полярные координаты,
Если а=b, Э. представляет собой окружность; - центр окружности, a - ее радиус, e=0, директрис нет.
Э. обладает следующим оптическим свойством: световые лучи, исходящие из одного фокуса, после зеркального отражения от Э. проходят через другой фокус.
Линия второго порядка, канонич. уравнение к-роп имеет вид

где а и b - действительные числа, наз. мнимым эллипсом.

А. Б. Иванов.