Akademik

- дополнительные к Эйлера уравнению необходимые условия экстремума, задаваемые в точках, где экстремаль имеет излом. Пусть

- функционал классического вариационного исчисления, а экстремаль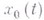. непрерывно дифференцируема в окрестности точки за исключением самой точки 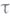, где 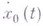имеет разрыв. Тогда для того чтобы давала хотя бы слабый локальный экстремум функционалу необходимо, чтобы в угловой точке выполнялись равенства

где

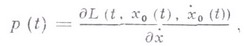
а

Эти равенства и наз. угловыми условиями Вейерштрасса - Эрдмана (К. Вейерштрасс, К. Weierstrass, 1865; Г. Эрдман, 1877, см. [1]).

В. -Э. у. у. означают непрерывность в угловой точке экстремали канонич. переменных и гамильтониана; в класснч. механике они означают непрерывность в угловой точке импульсов п энергии.

В регулярных задачах, когда 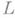- строго выпуклая по хфункция, экстремали не могут иметь угловых точек. Угловые точки появляются, когда 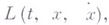а следовательно, и Вейерштрасса -функция содержат отрезки по . В случае, когда рассматривается Лаг-ранжа задача с ограничениями и Лагран-жа множителями . - Э. у. у. заменяется на

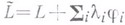
Лит.: [1] Erdmann G., "J. fur Math.", 1877, Bd 82, S. 21-30; [2] Во1zа О., Vorlesungen iiber Variationsrechnimg, Lpz., 1949, S. 367; [3] Axиезер Н. И.. Лекции по вариационному исчислению, М., 1955, с. 17-18. В. М. Тихомиров.