Akademik

в группу - мономорфизм полугруппы в группу. Полугруппа Sвкладывается в группу G, если Sизоморфна подполугруппе группы G. Необходимые и достаточные условия В. п. в группу были найдены А. И. Мальцевым [1] (см. также [3], с. 286). Эти условия представляют собой бесконечную систему условных тождеств ( квазитождеств), среди к-рых, в частности, имеются следующие:

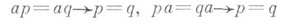
(законы сокращения);

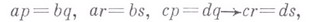
где 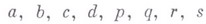- элементы полугруппы. Класс полугрупп, вложимых в группы, нельзя охарактеризовать конечным числом условных тождеств [2]. Известен ряд достаточных условий В. п. в группу. Наиболее важными из них являются следующие. Если S - полугруппа с сокращением и для любых элементов а, b полугруппы Sнайдутся элементы

такие, что 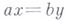(условие Оре), то полугруппа Sвложима в группу. Если S - полугруппа с сокращением, в к-рой из равенства всегда следует, что либо , либо для нек-рого элемента , то полугруппа Sвложима в группу [4]. Известны достаточные условия В. ц., сформулированные на языке теории графов (см., напр., [5]).

Лит.:[1] Мальцев А. И., "Матем. сб.", 1939, т. 6 (48), с. 331-36; [2] его же, там же, 1940, т. 8(50), с. 251-64; [3] Кон П. М., Универсальная алгебра, пер. с англ., М., 1968; [4] Doss R., "Bull. Sci. Math.", 1948, v. 72, p. 139- 150; [5] Адян С. И., Труды матем. ин-та АН СССР, 1966, т. 85, с. 1 -123. Л. А. Бокуть.