- теоремы, относящиеся к циклу вопросов, посвященных изучению неравенств между нормами одной и той же функции, принадлежащей к разным классам (нормированным пространствам). Обычно речь идет о двух классах 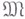 и
и 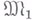 , где
, где  есть часть
есть часть  и при этом выполняется неравенство
и при этом выполняется неравенство
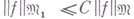
для всех 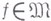 , где С - константа, не зависящая от
, где С - константа, не зависящая от 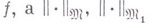 - нормы соответственно в
- нормы соответственно в  . При указанных условиях говорят, что имеет место вложение
. При указанных условиях говорят, что имеет место вложение 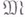 в
в 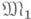 или, что
или, что 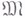 вкладывается в
вкладывается в 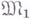 , и пишут
, и пишут  . Исследования, связанные с В. т., составляют раздел теории функций, но главные направления в них развиваются под влиянием краевых задач математической физики, в частности прямых вариационных методов. В связи с этим в течение последних трех десятилетий создана стройная теория вложений классов дифференцируемых функций многих переменных.
. Исследования, связанные с В. т., составляют раздел теории функций, но главные направления в них развиваются под влиянием краевых задач математической физики, в частности прямых вариационных методов. В связи с этим в течение последних трех десятилетий создана стройная теория вложений классов дифференцируемых функций многих переменных.
К числу задач, решаемых В. т., относятся, напр., следующие. Пусть известно, что функция f имеет частные производные порядка l, вообще говоря, обобщенные (см. Обобщенная производная), интегрируемые в р-й степени на данной области 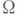 n-мерного пространства
n-мерного пространства 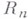 . Спрашивается: 1) какое гарантированное число непрерывных производных имеет эта функция на
. Спрашивается: 1) какое гарантированное число непрерывных производных имеет эта функция на 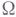 ? 2) если область
? 2) если область  имеет достаточно гладкую границу Г, то можно ли в том или ином смысле определить след
имеет достаточно гладкую границу Г, то можно ли в том или ином смысле определить след 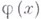 функции f в точках
функции f в точках  , т. е. предельные значения
, т. е. предельные значения  , когда
, когда 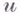 приближается к x, и какими гарантированными дифференциальными свойствами обладает этот след? При этом часто надо знать эти свойства настолько точно, чтобы наличие таковых у функции
приближается к x, и какими гарантированными дифференциальными свойствами обладает этот след? При этом часто надо знать эти свойства настолько точно, чтобы наличие таковых у функции 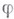 , заданной на Г, влекло возможность продолжения
, заданной на Г, влекло возможность продолжения 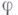 с Г на
с Г на 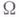 так, чтобы продолженная функция имела на
так, чтобы продолженная функция имела на 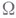 обобщенные производные порядка l, интегрируемые в р-йстепени. Из фактов, приводимых ниже, будет видно, что указанные пределы (понимаемые в смысле сходимости почти всюду) определения следа
обобщенные производные порядка l, интегрируемые в р-йстепени. Из фактов, приводимых ниже, будет видно, что указанные пределы (понимаемые в смысле сходимости почти всюду) определения следа 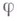 функции f и продолжения
функции f и продолжения 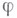 могут сопровождаться неравенствами между нормами fна
могут сопровождаться неравенствами между нормами fна  и Г, к-рые и применяются в теории краевых задач.
и Г, к-рые и применяются в теории краевых задач.
Многомерная теория вложений классов дифференцируемых функций возникла в 30-х гг. 20 в. в работах С. Л. Соболева в связи с решением задач математич. физики. Ему принадлежат основные В. т. для классов 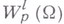 ( Соболева пространств), играющих важную роль в анализе. Функция
( Соболева пространств), играющих важную роль в анализе. Функция 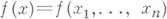 принадлежит
принадлежит 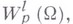
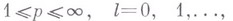 если она определена на
если она определена на 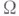 и для нее конечна норма
и для нее конечна норма
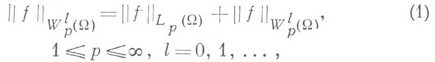
где

и сумма распространена на всевозможные (обобщенные по Соболеву) частные производные
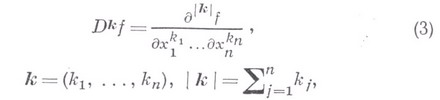
порядка  .
.
Основная теорема С. Л. Соболева (с дополнениями В. И. Кондрашова и В. П. Ильина) для случая  :
:
при условиях 
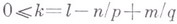 справедливо вложение
справедливо вложение

где [k]- целая часть k.
При  это означает, что функция
это означает, что функция 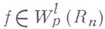 имеет след (см. ниже) на любой координатной гиперплоскости
имеет след (см. ниже) на любой координатной гиперплоскости  размерности т,
размерности т,
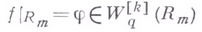
а
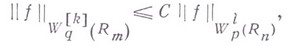
где Сне зависит от f (см. [6], [7]).
Функция f, заданная на 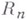 , имеет след на
, имеет след на 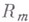 , где
, где 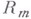 есть m-мерное (координатное) подпространство точек
есть m-мерное (координатное) подпространство точек 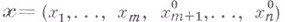 с фиксированными
с фиксированными  если f можно видоизменить на нек-ром множестве n-мерной меры нуль так, чтобы для видоизмененной функции, к-рая снова обозначается через f, имело место
если f можно видоизменить на нек-ром множестве n-мерной меры нуль так, чтобы для видоизмененной функции, к-рая снова обозначается через f, имело место

Если 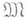 есть множество функций f, заданных на
есть множество функций f, заданных на 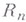 , то задача описания свойств следов этих функций на подпространство
, то задача описания свойств следов этих функций на подпространство 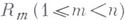 наз. проблемой следов для класса
наз. проблемой следов для класса 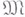 .
.
Теорема (4) является окончательной в терминах классов 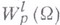 . Дальнейшее ее улучшение возможно лишь путем введения новых классов.
. Дальнейшее ее улучшение возможно лишь путем введения новых классов.
В одномерном случае 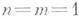 , где проблема следов не возникает, теорема (4) принадлежит Г. Харди и Дж. Литлвуду (G. Hardy, J. Littlewood).
, где проблема следов не возникает, теорема (4) принадлежит Г. Харди и Дж. Литлвуду (G. Hardy, J. Littlewood).
Следующим этапом в развитии этой теории являются теоремы вложения С. М. Никольского для обобщенных гёльдеровых классов (см. Гёльдерово пространство)( Н- классов). Эти классы образуют шкалу с непрерывно меняющимися параметрами, характеризующими гладкость функций. Они анизотропны в том смысле, что принадлежащие к ним функции обладают, вообще говоря, разными дифференциальными свойствами по разным направлениям. Пусть  есть множество точек
есть множество точек  , удаленных от границы
, удаленных от границы  больше чем на
больше чем на  , и пусть
, и пусть  - положительный вектор (
- положительный вектор ( ;
;  ),
),  - целое и
- целое и  .
.
Функция принадлежит классу 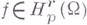 ,
, 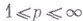 , если
, если 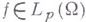 и для любого
и для любого  существует обобщенная частная производная
существует обобщенная частная производная

удовлетворяющая неравенству
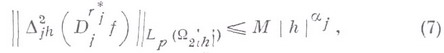
где 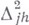 - вторая разность функции по переменной
- вторая разность функции по переменной 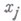 с шагом h и М- константа, не зависящая от h. Класс
с шагом h и М- константа, не зависящая от h. Класс 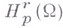 образует банахово пространство, если ввести норму
образует банахово пространство, если ввести норму

где 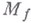 - наименьшая константа М, при к-рой выполняются неравенства (7). Для
- наименьшая константа М, при к-рой выполняются неравенства (7). Для 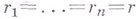 соответствующий (изотропный) класс обозначается через
соответствующий (изотропный) класс обозначается через 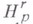 При целом lкласс
При целом lкласс 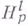 близок к классу Соболева
близок к классу Соболева 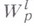 с точностью до
с точностью до  в том смысле, что
в том смысле, что
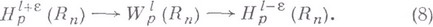
Справедливы теоремы вложения (С. М. Никольский)
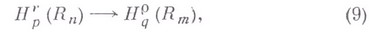
где
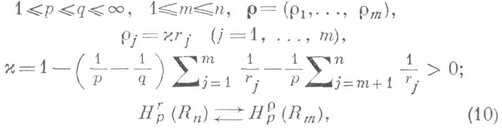
где
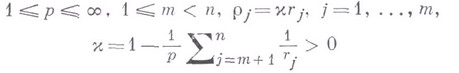
(см. [5]).
Теорема (9) является анизотропным аналогом теоремы (4), но имеет то преимущество, что верхние (векторные) индексы г, 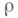 фигурирующих в ней классов могут изменяться непрерывно. Кроме того, она полностью охватывает случаи
фигурирующих в ней классов могут изменяться непрерывно. Кроме того, она полностью охватывает случаи  . Однако при
. Однако при 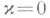 она, в отличие от (4), неверна. В одном случае ( п=т=1).при
она, в отличие от (4), неверна. В одном случае ( п=т=1).при 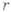 и
и 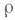 не целых она доказана Г. Хардп и Дж. ЛитлвуДОМ .
не целых она доказана Г. Хардп и Дж. ЛитлвуДОМ .
Частный случай теоремы (9) при  записан еще раз в виде вложения (10) с верхней стрелкой. Оно гласит: функция
записан еще раз в виде вложения (10) с верхней стрелкой. Оно гласит: функция  имеет след
имеет след  на
на  и при этом
и при этом
где Сне зависит от f. Но справедливо и обратное утверждение, выражаемое нижней стрелкой, к-рое надо понимать в следующем смысле: каждая определенная на 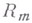 функция
функция 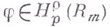 может быть продолжена на все пространство
может быть продолжена на все пространство  так, что полученная функция
так, что полученная функция 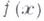 (со следом на
(со следом на 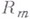 , равным
, равным 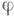 ) принадлежит к
) принадлежит к 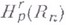 и выполняется неравенство (обратное к (11)):
и выполняется неравенство (обратное к (11)):
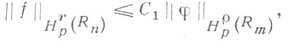
где 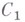 не зависит от
не зависит от 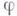 .
.
Взаимно обратные вложения (10) полностью решают проблему следов для H-классов и при этом в терминах H-классов.
Теорема (9) носит транзитивный характер, заключающийся в том, что переход

от первого класса в цепи (12) ко второму, а затем от второго к третьему, где параметры 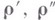 вычисляются по указанным в (9) формулам, может быть заменен одним переходом от первого класса к третьему при непосредственном вычислении
вычисляются по указанным в (9) формулам, может быть заменен одним переходом от первого класса к третьему при непосредственном вычислении 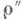 по тем же формулам.
по тем же формулам.
В дальнейшем (см. далее [14]) была решена проблема следов для W-классов, вообще анизотропных. Это привело к введению нового семейства классов дифференцируемых функций многих переменных 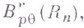 зависящих от векторного параметра rи двух скалярных параметров
зависящих от векторного параметра rи двух скалярных параметров  удовлетворяющих неравенствам
удовлетворяющих неравенствам 
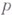 ,
,  .Во всей полноте это семейство определил О. В. Бесов, изучивший также его основные свойства.
.Во всей полноте это семейство определил О. В. Бесов, изучивший также его основные свойства.
Функция f при надлежит классу 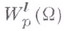 , где
, где 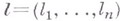 - целый вектор, если для нее имеет смысл конечная норма
- целый вектор, если для нее имеет смысл конечная норма
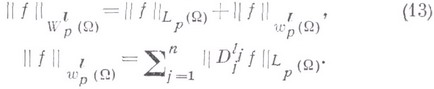
Функция fпринадлежит классу 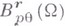 , где
, где  - произвольный, не обязательно целый вектор,
- произвольный, не обязательно целый вектор,  если для нее конечна норма
если для нее конечна норма

где числа 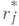 и
и 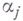 определены выше.
определены выше.
Естественно считать, что класс 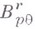 при
при  совпадает с классом
совпадает с классом 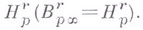 Обычно пишут еще
Обычно пишут еще  вместо
вместо 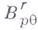 , когда
, когда 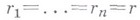 и
и 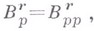
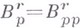 . Для любых указанных
. Для любых указанных  классы
классы 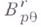 суть банаховы пространства.
суть банаховы пространства.
Теоремы вложения (9), (10) верпы, если в них заменить Нна В. Имеют место также взаимно обратные вложения
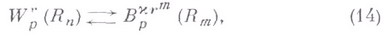
где 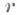 - целое,
- целое, полностью решающие проблему
полностью решающие проблему 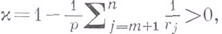 следов для W-классов, что не мешает выполняться взаимно обратным вложениям, выраженным полностью на языке В-классов:
следов для W-классов, что не мешает выполняться взаимно обратным вложениям, выраженным полностью на языке В-классов:

Классы 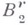 . соответствующие значениям параметров
. соответствующие значениям параметров
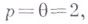 принято еще обозначать через
принято еще обозначать через 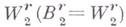 При
При 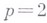 вложения (14) записываются еще и так
вложения (14) записываются еще и так
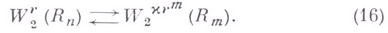
Естественными продолжениями W-классов являются классы, в определении к-рых фигурирует понятие дробной производной по Лиувнллю (см. Дробное интегрирование и дифференцирование).
Употребляя терминологию обобщенных функций, можно задать основной класс 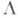 функций так, что построенный над ним класс
функций так, что построенный над ним класс 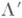 обобщенных функций будет обладать следующими свойствами: 1)
обобщенных функций будет обладать следующими свойствами: 1) 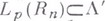 при любом конечном
при любом конечном  ; 2) при любом
; 2) при любом  ", не обязательно целом, имеет смысл операция
", не обязательно целом, имеет смысл операция

где 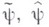 означают соответственно прямое и обратное Фуръе преобразование
означают соответственно прямое и обратное Фуръе преобразование ; 3) если l - целое и функция
; 3) если l - целое и функция  имеет обобщенную по Соболеву производную
имеет обобщенную по Соболеву производную 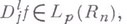 то для нее имеет место равенство (17).
то для нее имеет место равенство (17).
При дробных l на бесконечно дифференцируемых финитных функциях операция (17) совпадает с операцией дробного дифференцирования по Лиувнллю. Естественно называть 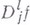 при нецелом lдробной производной от f порядка lпо
при нецелом lдробной производной от f порядка lпо  .
.
Если теперь задан произвольный вектор  то можно ввести пространство
то можно ввести пространство 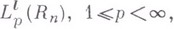 совпадающее с
совпадающее с 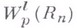 при целых
при целых 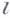 , заменив в (13)
, заменив в (13) на L.
на L.
Если 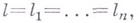 то положим
то положим 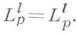 Семейство классов
Семейство классов  может рассматриваться как естественное расширение семейства
может рассматриваться как естественное расширение семейства 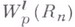 на дробное
на дробное 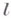 , "естественное" потому, что с точки зрения интересующего нас круга идей классы
, "естественное" потому, что с точки зрения интересующего нас круга идей классы 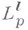 обладают "всеми достоинствами и недостатками классов
обладают "всеми достоинствами и недостатками классов  ". Если в формуле (4) (где [k]можно заменить на k), или (8) (где lможет быть дробным), или в (14), (16) (где
". Если в формуле (4) (где [k]можно заменить на k), или (8) (где lможет быть дробным), или в (14), (16) (где 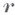 может быть дробным) заменить Wна L, то они останутся верными. Верной также останется формула (9), если в пей заменить Нна Lдаже при более широком условии
может быть дробным) заменить Wна L, то они останутся верными. Верной также останется формула (9), если в пей заменить Нна Lдаже при более широком условии  однако в предположении, что
однако в предположении, что 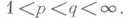
В дальнейшем продолжается применение аппарата обобщенных функций, но теперь уже составляющих пространство 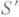 . Для любого действительвого числа р имеет смысл операция (Бесселя - Макдональда):
. Для любого действительвого числа р имеет смысл операция (Бесселя - Макдональда):
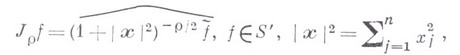
обладающая свойствами:
 - оператор Лапласа.
- оператор Лапласа.
Изотропный класс 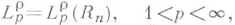 может быть определен еще как совокупность функций f, пред-(лавимых в виде
может быть определен еще как совокупность функций f, пред-(лавимых в виде 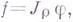 где функции
где функции  пробегают пространство
пробегают пространство 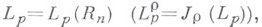 при этом, с точностью до эквивалентности,
при этом, с точностью до эквивалентности,
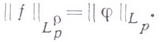
Это определение класса 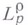 годится и для отрицательных
годится и для отрицательных 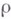 , но в этом случае
, но в этом случае 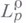 есть совокупность, вообще говоря,
есть совокупность, вообще говоря, 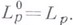 обобщенных функций . В частности
обобщенных функций . В частности  .
.
Операция 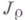 может служить средством и для определения классов
может служить средством и для определения классов 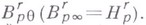 Именно, будем называть обобщенную функцию
Именно, будем называть обобщенную функцию 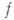 регулярной в смысле
регулярной в смысле 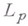 или принадлежащей к
или принадлежащей к  , если найдется такое
, если найдется такое  , что
, что  Всякую функцию
Всякую функцию 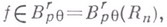
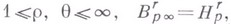 можно определить как регулярную в смысле
можно определить как регулярную в смысле 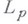 функцию, представимую рядом
функцию, представимую рядом
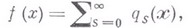
слабо сходящимся к 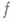 (в смысле
(в смысле  ), где
), где 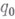 имеет спектр (носитель
имеет спектр (носитель 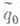 ) в
) в  , а
, а  при
при  имеет спектр в
имеет спектр в  и
и
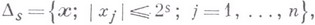
и при этом

В частности,
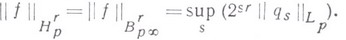
Это определение класса 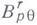 автоматически распространяется на случай
автоматически распространяется на случай  , и тогда функции f, входящие в эти классы, будут, вообще говоря, обобщенными (
, и тогда функции f, входящие в эти классы, будут, вообще говоря, обобщенными ( ). При этом
). При этом  .
.
Существуют и другие эквивалентные определения отрицательных классов 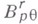 , основанные на принципе интерполяции функциональных пространств. Приведенное определение носит конструктивный характер - каждый заданный параметрами
, основанные на принципе интерполяции функциональных пространств. Приведенное определение носит конструктивный характер - каждый заданный параметрами 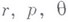 класс определяется независимо, при этом можно конструктивно определить линейные операции, при помощи к-рых по данной функции
класс определяется независимо, при этом можно конструктивно определить линейные операции, при помощи к-рых по данной функции  определяется функция
определяется функция 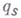 (экспоненциального типа
(экспоненциального типа 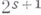 при
при  и типа 1 при s=0).
и типа 1 при s=0).
Справедлива теорема вложения:
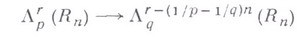
типа теоремы (4), но с  , верная при любом действительном r для
, верная при любом действительном r для 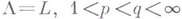 или для
или для 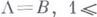
 или для
или для 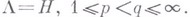
С другой стороны, при 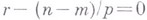 произвольная функция
произвольная функция  , вообще говоря, не имеет следа на
, вообще говоря, не имеет следа на 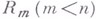 , если не налагать на нее дополнительных условий.
, если не налагать на нее дополнительных условий.
Выше были сформулированы В. т. для классов функций, определенных на всем n-мерном пространстве  (см. [5]). Но для приложений важно иметь подобные теоремы для возможно общпх областей
(см. [5]). Но для приложений важно иметь подобные теоремы для возможно общпх областей  . В настоящее время выяснена геометрич. структура областей
. В настоящее время выяснена геометрич. структура областей  , для к-рых верны указанные теоремы вложения для W-, В- и H-классов, где надо заменить
, для к-рых верны указанные теоремы вложения для W-, В- и H-классов, где надо заменить  соответственно на
соответственно на 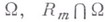 . Для изотропных классов
. Для изотропных классов  ,
, 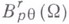 область
область 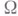 должна удовлетворять условию конуса или, что равносильно, граница ее должна удовлетворять локально условию Липшица. Для анизотропных же классов
должна удовлетворять условию конуса или, что равносильно, граница ее должна удовлетворять локально условию Липшица. Для анизотропных же классов 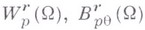 область
область  должна удовлетворять условию
должна удовлетворять условию 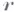 -рога или изогнутого конуса ( конуса условие). и это условие является в известном смысле необходимым (см. [2]).
-рога или изогнутого конуса ( конуса условие). и это условие является в известном смысле необходимым (см. [2]).
Для приложений важна еще проблема о следах на m-мерных многообразиях 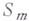 .
.
Для изотропных классов W, Н, В эта проблема решена полностью (см. [2], [16]), если 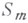 достаточно много раз дифференцируемо при
достаточно много раз дифференцируемо при 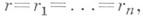 в (14), (15) и (16) можно заменить
в (14), (15) и (16) можно заменить 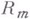 на
на  , а в (19), кроме того, можно заменить Я на В. В случае кусочно гладких
, а в (19), кроме того, можно заменить Я на В. В случае кусочно гладких 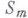 этот вопрос тоже в ряде случаев решен до конца ([16], [22]), условия, решающие проблему, выражаются, с одной стороны, указанными выше взаимно обратными вложениями на отдельных гладких кусках
этот вопрос тоже в ряде случаев решен до конца ([16], [22]), условия, решающие проблему, выражаются, с одной стороны, указанными выше взаимно обратными вложениями на отдельных гладких кусках 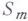 , а с другой- специальными дополнительными условиями на поведение функций соответствующих классов на стыках этих гладких кусков. Существенно продвинута также проблема следов для анизотропных классов ([9], [21] ). Здесь возникают особые затруднения характеристики следа в точках
, а с другой- специальными дополнительными условиями на поведение функций соответствующих классов на стыках этих гладких кусков. Существенно продвинута также проблема следов для анизотропных классов ([9], [21] ). Здесь возникают особые затруднения характеристики следа в точках 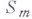 , касательные плоскости к к-рым параллельны осям координат.
, касательные плоскости к к-рым параллельны осям координат.
Остановимся еще на одной задаче. Пусть функция
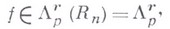
где 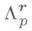 означает один из рассмотренных выше классов. Спрашивается, какие она имеет частные смешанные производные
означает один из рассмотренных выше классов. Спрашивается, какие она имеет частные смешанные производные 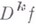 и каковы пх свойства? Положительный ответ на этот вопрос зависит от величины
и каковы пх свойства? Положительный ответ на этот вопрос зависит от величины
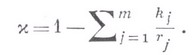
Именно, если  то существует частная производная
то существует частная производная 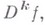 принадлежащая к пространству
принадлежащая к пространству  при условии, что
при условии, что 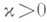 . В случае же пространств
. В случае же пространств 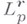 это условие можно расширить, считая
это условие можно расширить, считая  (см. [5]).
(см. [5]).
Приведем еще характерную теорему, к-рую естественно назвать теоремой об ослабленной компактности и к-рая имеет применение в теории прямых методов вариационного исчисления.
Из бесконечного множества 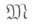 функции f, удовлетворяющих неравенству
функции f, удовлетворяющих неравенству
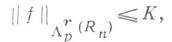
где 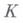 - заданная константа, а
- заданная константа, а  - один из рассмотренных выше классов, можно выделить последовательность
- один из рассмотренных выше классов, можно выделить последовательность 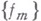 функций и указать такую функцию
функций и указать такую функцию  с нормой
с нормой

что какова бы ни была ограниченная область  ц вектор
ц вектор 
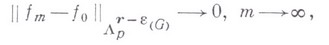
(см. [5]). В этой формулировке  может быть заменено на область
может быть заменено на область  , если она имеет достаточно хорошую границу. Выше были рассмотрены только характерные классы функций и связанные с ними теоремы вложения, наиболее часто встречающиеся в приложениях. В современных исследованиях большое внимание [2] уделяется классам более общим, где роль исходных частных производных
, если она имеет достаточно хорошую границу. Выше были рассмотрены только характерные классы функций и связанные с ними теоремы вложения, наиболее часто встречающиеся в приложениях. В современных исследованиях большое внимание [2] уделяется классам более общим, где роль исходных частных производных 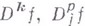 играют более или менее произвольные дифференциальные операторы.
играют более или менее произвольные дифференциальные операторы.
Изучаются еще так наз. весовые классы, характерным примером к-рых является класс 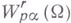 , определяемый следующим образом. Пусть
, определяемый следующим образом. Пусть 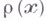 есть расстояние от точки ждо границы Г области
есть расстояние от точки ждо границы Г области 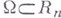 . Функция f принадлежит к
. Функция f принадлежит к  если для нее конечна норма (см. [4], [12])
если для нее конечна норма (см. [4], [12])

где
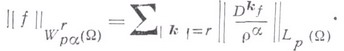
Приведем только один результат. .Пусть 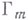 - достаточно гладкая граница тизмерений; тогда
- достаточно гладкая граница тизмерений; тогда
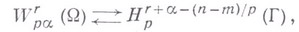
если 
Пример. Использование В. т. полностью решает вопрос об условиях на граничную функцию, при к-рых применим Дирихле принцип. Именно, понимая частные производные в обобщенном смысле и считая для простоты, что поверхность Г (граница трехмерной области) ограничена и дважды дифференцируема, задаем на  функцию
функцию 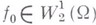 . Для нее Дирихле интеграл
. Для нее Дирихле интеграл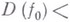
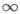 и, кроме того, по В. т.
и, кроме того, по В. т.

 имеет след на Г (факт существования следа у
имеет след на Г (факт существования следа у 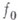 устанавливался при помощи более грубых В. т.). Обозначив через
устанавливался при помощи более грубых В. т.). Обозначив через 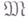 класс функций
класс функций 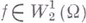 , имеющих тот же след на Г, что и
, имеющих тот же след на Г, что и  можно сформулировать принцип Дирихле следующим образом: минимум
можно сформулировать принцип Дирихле следующим образом: минимум  среди функций
среди функций 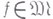 достигается для единственной функции и к тому же гармонической на
достигается для единственной функции и к тому же гармонической на  . Из приведенной В. т. следует, что принцип Дирихле применим тогда и только тогда, когда класс
. Из приведенной В. т. следует, что принцип Дирихле применим тогда и только тогда, когда класс 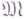 не пуст, т. е. когда граничная функция
не пуст, т. е. когда граничная функция 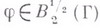
При обосновании принципа Дирихле сначала доказывается существование и единственность функции  , а также тот факт, что иесть обобщенное решение задачи Дирихле, а затем при помощи специального метода последовательно устанавливается, что обобщенное решение принадлежит классам
, а также тот факт, что иесть обобщенное решение задачи Дирихле, а затем при помощи специального метода последовательно устанавливается, что обобщенное решение принадлежит классам  , где
, где 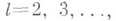 а
а  - произвольный замкнутый шар. В частности, из того факта, что
- произвольный замкнутый шар. В частности, из того факта, что  , на основании В. т.
, на основании В. т.
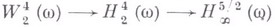
(см. [2] и [5]) при 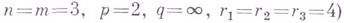 заключаем, что функцию иможно видоизменить на множестве трехмерной меры нуль так, чтобы полученная функция была дважды непрерывно дифференцируема на
заключаем, что функцию иможно видоизменить на множестве трехмерной меры нуль так, чтобы полученная функция была дважды непрерывно дифференцируема на  . После этого легко доказывается, что
. После этого легко доказывается, что 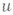 -гармоническая.
-гармоническая.
Приведенный пример может быть значительно обобщен на нек-рые функционалы, в к-рые входят частные производные разных порядков, возведенные в степень, вообще не равную 2 ( ), и тогда появляется необходимость применения В. т. для более общих классов, вообще говоря, анизотропных.
), и тогда появляется необходимость применения В. т. для более общих классов, вообще говоря, анизотропных.
Лит.:[1] Сб. дифференциальные уравнения с частными производными, М., 1970, с. 38-63; [2] Бесов О. В., Ильин В. П., Никольский С. М., Интегральные представления функций и теоремы вложения, М., 1974; [3] Буренков В. И., Теоремы вложения и продолжения для классов дифференцируемых функций многих переменных во всем пространстве, в кн.: Итоги науки. Математический анализ. 1965, М., 1966: [4] Никольский С. М., "Успехи матем. наук", 1961, т. 16, в. 5, с. 63-114; [5] его же. Приближение функции многих переменных и теоремы вложения, М., 1969; [6] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Л., 1950 [7] его же. Введение в теорию кубатурных формул, М., 1974: [8] Бесов О. В., "Труды Матем. ин-та АН СССР", 1961, г. 60, с. 42-81; [9] Бугров Я. С., "Сиб. матем. ж.", 1964, г. 5, № 5, с. 1007-26; [10] Ильин В. П., "Докл. АН СССР", 1954, т. 96, № 5, с. 905-8; [11] Кондратов В. И., там же, 1945, т. 48, с. 563-6; [12] Кудрявцев Л. Д., "Труды Матем. Ин-та АН СССР", 1959, т. 55, с. 1 - 182; [13] Лизоркин П. И., "Докл. АН СССР", 1960, т. 132, № 3, с. 514-17; [14] его же, "Матем. сб.",
1963, т. 60, в. 3, с. 325-53; [15] Никольский С. М., "Труды Матем. ин-та АН СССР", 1951, т. 38, с. 244-78; [16] его же, "Матем. сб.", 1953, т. 33, в. 2, с. 261-326; 1957, т. 43, в. 7, с. 127-44; [17] Соболев С. Л., "Докл. АН СССР", 1935, т. 3, JV" 7, с. 291-4; [18] его же, "Матем. сб.", 19.46, т. 1, в. 1, с. 39-72; 1938, т. 4, в. 3, с. 471-97; [19] Слободецкий Л. Н., "Докл. АН СССР", 1958, т. 118, в. 2, с. 243-6; [20] Успенский С. В., "Труды Матем. ин-та АН СССР", 1961, т. 60, с. 282-303; [21] его же, "Докл. АН СССР", 1965, т. 164, № 4, с. 750-2: [22] Яковлев Г. Н., "Труды Матем. ин-та АН СССР", 1961, т. 60, с. 325-49; [23] Gagliardo Е., "Rend Semin. matem. in-ta di Padova", 1957, t. 27, p. 284- 305; [24] Hardу G. H., Lilttlewood J.E., "Math. Z.", 1928, Bd 28, №4, S. 612 - 34: [25] Lions J. L., Ma genes E., Problemes aux limites non homogebes et applications, P., 1968, v. 1-2. С. М. Никольский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.