такая функция f(x), определенная на нек-ром числовом множестве Е, что из условия
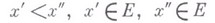
следует:
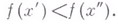
Иногда такие функции наз. строго возрастающими, а термин "В. ф." применяется к функциям, удовлетворяющим для указанных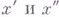 
лишь условию 
(неубывающие функции). У всякой строго В. ф. обратная функция является однозначной н также строго возрастающей. Если 
- правосторонняя (соответственно, левосторонняя) предельная точка множества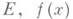 
- неубывающая функция и множество 
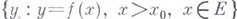ограничено снизу (соответственно 
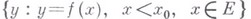ограничено сверху), то при 
(соответственно, при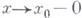 
), 
, у функции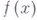 
существует конечный предел; если же указанное множество не ограничено снизу (соответственно, сверху), то 
имеет бесконечный предел, равный 
(соответственно, 
).
Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.