Akademik

- частный случай движения, при к-ром по крайней мере одна точка пространства остается неподвижной. При В. плоскости неподвижная точка наз. центром вращения, при В. пространства неподвижная прямая - осью вращения. В. евклидова пространства наз. собственным (В. 1-го рода), или несобственным (В. 2-го рода) в зависимости от того, сохраняет оно или не сохраняет ориентацию пространства.

На плоскости собственное В. выражается аналитически в декартовых прямоугольных координатах ( х, у).при помощи формул (начало координат в центре В.)

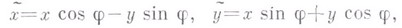
где - угол поворота. Собственное В. на угол может быть представлено как произведение двух осевых симметрии с осями, пересекающимися под углом .

Несобственное В. на плоскости выражается аналитически в декартовых прямоугольных координатах ( х, у).при помощи формул (начало координат в центре В.):

где ,- угол поворота. Несобственное В. на плоскости может быть представлено как произведение собственного В. на осевую симметрию.

В случае n-мерного евклидова пространства В. аналитически выражается с помощью ортогональной матрицы, к-рая приводится к канонич. виду:

где

- единичная матрица порядка . Возможны следующие случаи:

1) р=n - тождественное преобразование;

2) q=n - В. является центральной симметрией;

3) p+q=п- В. является симметрией относительно р-плоскости (отражением от р-плоскости);

4) Мне содержит подматриц и - - В. наз. поворотом вокруг единственной неподвижной точки;

5) Мсодержит подматрицы и , но не содержит подматрицу - - В. наз. поворотом вокруг р-плоскости;

6) Мсодержит подматрицы и -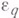, но не содержит подматрицы - В. наз. поворотным отражением от ( п- q )-п лоскости.

В. евклидова пространства вокруг данной точки образует группу относительно операции умножения В., изоморфную группе ортогональных преобразований Векторного пространства или группе ортогональных матриц порядка пнад полем R. Группа В. пространства является -мерной группой Ли и действует в ЕД интранзитивно.

Лит.:[1] Роаенфельд Б. А., Многомерные пространства, М., 1966; [2] его же, Неевклидовы пространства М., 1969; [3] Широков П. А., Тензорное исчисление. Алгебра тензоров, 2 изд., Казань, 1961. В. Т. Базылев